Циклическая частота – это одна из основных характеристик колебательных процессов, которая позволяет определить количество полных колебаний, происходящих за единицу времени. Она широко применяется в физике, инженерии, электронике и других науках, где изучаются колебательные системы.
Для получения значения циклической частоты, используется специальная формула, которая связывает ее с периодом колебаний. Обычно обозначается символом ω (омега) и измеряется в радианах в секунду или герцах. Формула для расчета циклической частоты имеет вид:
ω = 2π / T
где ω - циклическая частота, а T - период колебаний.
Примером использования циклической частоты может служить колебание маятника. Если известно значение периода колебаний, то можно легко определить циклическую частоту. Например, если период колебаний маятника составляет 2 секунды, то циклическая частота будет равна:
ω = 2π / 2 = π рад/с
Таким образом, значение циклической частоты позволяет установить количество полных колебаний, которые произойдут за единицу времени, что является важным параметром для анализа и проектирования различных колебательных систем.
Циклическая частота колебаний: основные понятия

ω = 2πf
где f – частота колебаний в герцах, а π ≈ 3.14159 – математическая константа «пи».
Циклическая частота является обратной величиной к периоду колебаний T и может быть выражена также как:
ω = 2π/T
где T – период колебаний, то есть время, за которое система совершает один полный цикл колебаний.
У циклической частоты есть связь с амплитудой колебаний и жесткостью системы. Она определяет быстроту, с которой система совершает колебания. Чем больше циклическая частота, тем чаще происходят колебания, и наоборот.
Примеры систем, подчиняющихся циклической частоте, включают маятники, колебательные цепи, электрические и механические резонаторы и т.д. Зная значения циклической частоты и других параметров системы, можно проводить анализ ее свойств и предсказывать поведение в разных условиях.
Циклическая частота: определение и значение
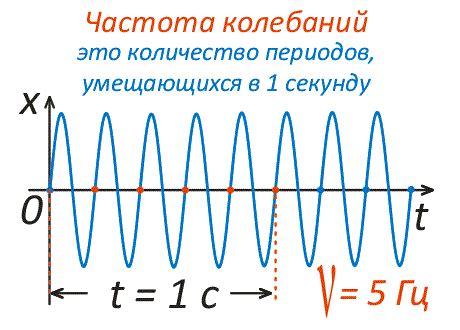
Циклическая частота является одной из основных характеристик системы колебаний. Она определяет скорость, с которой колеблющаяся система проходит через свои стабильные состояния. Чем выше циклическая частота, тем быстрее система совершает колебания.
Значение циклической частоты зависит от физических свойств системы и может быть вычислено по следующей формуле:
ω = 2πf
где ω – циклическая частота,
π – математическая константа, приблизительно равная 3.1416,
f – частота колебаний, измеряемая в герцах (Гц).
Пример: Пусть дана система, в которой частота колебаний равна 10 Гц. Тогда для определения циклической частоты нужно воспользоваться формулой:
ω = 2πf
ω = 2π * 10
ω ≈ 62.83 рад/с
Таким образом, в данном примере циклическая частота равна приблизительно 62.83 рад/с.
Формула циклической частоты колебаний

Циклическая частота (ω) колебаний определяется по формуле:
ω = 2πf,
где f - частота колебаний, а π (пи) - математическая константа (приближенное значение равно 3,14).
Формула позволяет вычислить циклическую частоту колебаний, используя известную частоту. Циклическая частота определяет, сколько полных колебаний происходит за одну секунду и измеряется в радианах в секунду. Чем выше частота, тем больше циклическая частота.
Как определить циклическую частоту на практике?

- Выберите систему, которая совершает колебания.
- Установите начальные условия для системы (например, задайте начальное положение и скорость).
- Измерьте время, за которое система совершает определенное число полных колебаний.
- Рассчитайте циклическую частоту по формуле:
Циклическая частота (ω) = 2π / период (T)
где период (T) - время, за которое система совершает одно полное колебание.
Например, если система совершает 5 полных колебаний за 2 секунды, то период равен 2 секунды / 5 колебаний = 0.4 секунды. Подставляя значение периода в формулу, получаем:
Циклическая частота (ω) = 2π / 0.4 секунды ≈ 15.708 рад/с
Таким образом, циклическая частота равна примерно 15.708 радиан в секунду.
Определение циклической частоты на практике позволяет узнать, как быстро система совершает колебания и может быть полезно, например, при проектировании механических систем или анализе электрических цепей.
Циклическая частота колебаний: примеры из физики

1. Механические колебания: например, колебания маятника. Циклическая частота маятника определяется его длиной и ускорением свободного падения. Частота колебаний маятника может быть найдена по формуле:
где - циклическая частота,
- ускорение свободного падения,
- длина маятника.
2. Электрические колебания: например, колебания в электрической цепи переменного тока. Циклическая частота этих колебаний определяется емкостью и индуктивностью цепи. Частота колебаний может быть найдена по формуле:
где - циклическая частота,
- индуктивность цепи,
- емкость цепи.
3. Акустические колебания: например, колебания в звуковой волне. Циклическая частота звуковой волны определяется скоростью распространения звука и длиной волны. Частота колебаний может быть найдена по формуле:
где - циклическая частота,
- скорость распространения звука,
- длина волны.
4. Оптические колебания: например, колебания электромагнитного поля в световой волне. Циклическая частота световой волны определяется скоростью света и длиной волны. Частота колебаний может быть найдена по формуле:
где - циклическая частота,
- скорость света,
- длина волны.




