Одно из базовых понятий в геометрии - это расположение точек относительно прямых. Очень важно знать, что значит, что точки лежат по одну сторону от прямой. Это позволяет нам определить свойства фигур, проводить разнообразные геометрические доказательства и решать задачи.
Точки могут лежать либо по одну сторону от прямой, либо по разные стороны. Если точки лежат по одну сторону, то мы говорим, что они образуют выпуклый угол. Если же точки лежат по разные стороны, мы получаем невыпуклый угол. Это понятие крайне полезно при изучении треугольников, так как можно определить, какой угол треугольника является выпуклым.
Давайте рассмотрим пример. Представим, что у нас есть прямая AB и точки C и D. Если точки C и D лежат по одну сторону от прямой AB, то мы можем с уверенностью сказать, что угол BAC и угол BAD являются выпуклыми углами. Это свойство можно использовать для доказательства различных теорем и задач геометрии.
Итак, знание того, что значит, что точки лежат по одну сторону от прямой, помогает нам лучше понимать геометрические объекты и выполнять различные операции с ними. Это позволяет проводить доказательства, решать задачи и изучать различные свойства фигур. Уверенное владение этим понятием открывает перед нами множество возможностей в изучении геометрии и повышает наши математические навыки.
Точки лежат по одну сторону - объяснение работы

Когда говорят, что точки лежат по одну сторону от прямой, это означает, что все эти точки находятся либо слева от нее, либо справа от нее. Итак, представьте себе прямую линию. Если все точки находятся на одной стороне от прямой, то можно сказать, что они лежат по одну сторону от нее.
Чтобы лучше понять, как работает эта концепция, рассмотрим следующий пример. Представьте, что у вас есть прямая линия, и на ней расположены точки A, B и C. Если точка A и точка B находятся по одну сторону от точки C, то можно сказать, что все три точки лежат по одну сторону от прямой.
То же самое можно применить и на практике. Например, предположим, что у вас есть задание найти все точки, которые лежат по одну сторону от прямой линии, проходящей через две известные точки. Вы можете просмотреть все остальные точки и проверить, находятся ли они по одну сторону от прямой или нет. Если они находятся по одну сторону, то они будут соответствовать условию задания.
Важно отметить, что при определении того, находятся ли точки по одну сторону от прямой, нужно учитывать направление прямой. Если вы меняете направление прямой, то и сторона, с которой будут определены точки, также изменится.
Понятие предиката и ориентированной площади
Одним из условий, использующих предикаты, является положение точек относительно прямой. Говорят, что точки лежат по одну сторону от прямой, если все они находятся либо справа, либо слева от нее. Если же среди точек имеются и такие, которые находятся с одной стороны прямой, а другие - с другой, то точки лежат по разные стороны от прямой. В случае, когда точки принадлежат прямой, говорят, что они лежат на прямой. Положение точек относительно прямой можно определить с помощью аналитических методов, например, вычисления координат точек и уравнения прямой.
Ориентированная площадь является еще одним понятием, связанным с положением точек. Она определяется путем сравнения площадей двух разных фигур, образованных одним и тем же участком пространства и разными наборами точек. В случае положительной ориентированной площади, фигура с левой стороны от прямой образует большую площадь, чем фигура с правой стороны, а в случае отрицательной ориентированной площади это наоборот. При вычислении ориентированной площади, часто используют векторное произведение векторов, определяющих различные точки.
Как определить, лежат ли точки по одну сторону
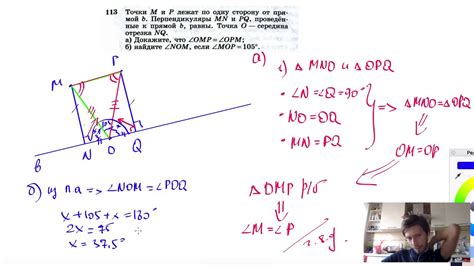
Для определения того, лежат ли точки по одну сторону от прямой, нужно применить следующий алгоритм:
- Выберите прямую, относительно которой вы будете проверять положение точек.
- Подставьте координаты точек в уравнение прямой и получите значения выражения.
- Если все значения выражения либо все положительны, либо все отрицательны, то точки лежат по одну сторону от прямой.
- Если значения выражения разные, то точки не лежат по одну сторону от прямой.
Примеры:
Пусть дана прямая с уравнением y = 2x + 1, и нам нужно определить, лежат ли точки (1,3), (2,5) и (3,7) по одну сторону от этой прямой. Подставим координаты точек в уравнение прямой:
- Для точки (1,3) получим: 3 = 2*1 + 1 = 3 (выражение равно 3, положительное значение)
- Для точки (2,5) получим: 5 = 2*2 + 1 = 5 (выражение равно 5, положительное значение)
- Для точки (3,7) получим: 7 = 2*3 + 1 = 7 (выражение равно 7, положительное значение)
Так как для всех точек значения выражения положительные и одинаковые, можно сделать вывод, что точки (1,3), (2,5) и (3,7) лежат по одну сторону от прямой y = 2x + 1.
Графическое представление и примеры

Чтобы лучше понять, что означает, что точки лежат по одну сторону от прямой, полезно представить это графически.
Представим, что у нас есть прямая и несколько точек. Если все точки находятся по одну сторону от прямой, то можно провести прямую так, чтобы она не пересекала ни одну из точек. Такое положение точек можно считать, например, "выше" или "ниже" относительно прямой.
Например, рассмотрим следующий график:
В данном примере все точки находятся выше прямой, и они лежат по одну сторону от нее.
Чтобы привести другой пример, представим, что есть прямая и две точки. Если одна точка находится ниже прямой, а другая выше, то они лежат по разные стороны от прямой.
В данном примере точка A находится ниже прямой, а точка B - выше, поэтому они лежат по разные стороны от прямой.
Таким образом, графическое представление позволяет наглядно определить, как лежат точки относительно прямой и понять, что значит, что точки лежат по одну сторону от прямой.






