Модуль разности чисел является одним из простейших математических операций, которую мы можем выполнить с двумя числами. Модуль разности чисел представляет собой абсолютное значение разности между этими числами.
Абсолютное значение числа - это положительное значение этого числа, независимо от его знака. Например, абсолютное значение числа -5 равно 5. Если мы вычисляем модуль разности чисел, то мы находим абсолютное значение разности между этими числами.
Модуль разности чисел может быть полезен во множестве ситуаций. Например, если мы занимаемся анализом данных и хотим узнать, насколько два числа отличаются друг от друга, мы можем использовать модуль разности чисел для получения точного значения этой разницы, независимо от знаков этих чисел.
Давайте рассмотрим несколько примеров. Пусть у нас есть два числа: 10 и 4. Чтобы найти модуль разности этих чисел, мы вычитаем одно число из другого и берем абсолютное значение разности. В данном случае, разность 10 и 4 равна 6. Модуль этой разности составляет 6.
Теперь рассмотрим другой пример. Пусть у нас есть два числа: -8 и 3. Если мы вычтем 3 из -8, получим -11. Однако, модуль этой разности будет равен 11, так как мы берем абсолютное значение разности.
Итак, модуль разности чисел позволяет нам определить абсолютное значение разности между двумя числами, независимо от их знаков. Это полезное математическое понятие, которое может быть применено во множестве областей и ситуаций.
Что такое модуль разности чисел: примеры и объяснение

Для вычисления модуля разности чисел применяется следующая формула:
|a - b|
Где a и b это два числа.
Например, пусть имеется два числа: 5 и 8. Их разность равна -3. Однако, модуль разности будет равен 3, так как модуль всегда возвращает положительное значение.
В другом примере, пусть у нас есть числа -10 и -2. Их разность также составляет -8. Однако, модуль разности будет равен 8, так как снова мы игнорируем знак и берем только абсолютное значение.
Модуль разности чисел может использоваться для решения различных математических задач, например, для нахождения расстояния между двумя точками на числовой прямой или для вычисления ошибки при сравнении двух величин.
Модуль разности чисел: определение и понятие

Модуль разности представляет собой положительное число, которое показывает насколько одно число различается от другого. Если результат разности положителен, то модуль разности будет равен этому положительному числу. Если же результат разности отрицателен, то модуль разности будет равен этому числу со знаком "+".
Модуль разности чисел обычно используется для нахождения расстояния между точками на числовой прямой или для определения величины ошибки или расхождения при сравнении двух числовых значений.
Для того чтобы найти модуль разности чисел, нужно выполнить следующие шаги:
| Шаг | Действие |
|---|---|
| 1 | Вычислить разность между двумя числами (a - b). |
| 2 | Применить операцию модуля к полученной разности (|a - b|). |
Например, для чисел a = 7 и b = 3 модуль разности будет равен |7 - 3| = |4| = 4. То есть, абсолютное значение разности между этими числами равно 4.
Таким образом, модуль разности чисел позволяет определить только величину разности без учета ее направления и знака. Он является полезным инструментом для анализа данных и решения различных математических задач.
Как найти модуль разности чисел: формула и методика

Чтобы найти модуль разности чисел, следует выполнить следующие шаги:
- Выбрать два числа, между которыми нужно найти разность.
- Вычесть из первого числа второе число.
- Взять абсолютное значение полученной разности.
Математическая формула для нахождения модуля разности чисел выглядит следующим образом:
| Модуль разности a и b | = | |a - b| |
Например, если заданы числа a = 5 и b = 8, то модуль разности можно найти следующим образом:
| Модуль разности 5 и 8 | = | |5 - 8| | = | |-3| | = | 3 |
Таким образом, модуль разности чисел 5 и 8 равен 3.
Умение находить модуль разности чисел полезно, например, при решении задач по алгебре, физике или программированию. Надеемся, что объяснение и примеры помогут вам легче разобраться с этой концепцией.
Примеры вычисления модуля разности чисел

Модуль разности чисел может быть вычислен путем взятия абсолютной величины разности чисел. Это значит, что результат всегда будет положительным числом или нулем. Ниже приведены несколько примеров вычисления модуля разности чисел:
Пример 1:
Даны два числа: 7 и 3. Для вычисления модуля разности чисел необходимо вычесть одно число из другого и взять абсолютное значение разности. В данном случае модуль разности чисел будет равен |7 - 3| = 4.
Пример 2:
Даны два числа: 15 и 20. Вычисляем разность чисел: 20 - 15 = 5. Затем берем абсолютное значение разности, чтобы получить модуль разности чисел: |20 - 15| = 5.
Пример 3:
Даны два числа: -10 и 5. Вычисляем разность чисел: 5 - (-10) = 15. Затем берем абсолютное значение разности, чтобы получить модуль разности чисел: |5 - (-10)| = 15.
Пример 4:
Даны два числа: 0 и 0. Вычисляем разность чисел: 0 - 0 = 0. Затем берем абсолютное значение разности, чтобы получить модуль разности чисел: |0 - 0| = 0.
Пример 5:
Даны два числа: 10 и -15. Вычисляем разность чисел: -15 - 10 = -25. Затем берем абсолютное значение разности, чтобы получить модуль разности чисел: |-15 - 10| = 25.
Таким образом, модуль разности чисел всегда будет положительным числом или нулем и позволяет получить абсолютное значение разности между двумя числами.
Зачем нужно находить модуль разности чисел: практическое применение
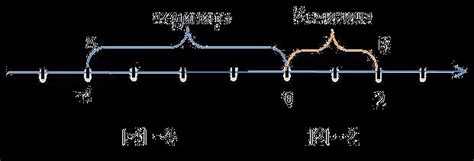
- Физика: Модуль разности двух векторов используется для определения расстояния между двумя точками в трехмерном пространстве. Это может быть полезно, например, при расчете разности пути или скорости движения тела.
- Техника: Нахождение модуля разности значений величин позволяет определить, насколько точно измеряемая величина соответствует эталону. Это может использоваться в калибровке приборов или контроле качества продукции.
- Экономика: Применение модуля разности чисел может быть полезно при анализе различных показателей, например, при сравнении динамики доходов и расходов компании за определенный период времени.
- Математика: В математике модуль разности чисел часто используется при решении задач на определение расстояния между точками на числовой прямой или в координатной плоскости.
В целом, нахождение модуля разности чисел позволяет получить абсолютное значение разности без учета ее знака. Это может быть полезно в различных ситуациях, когда необходимо получить положительное число или убрать учет направления. Практическое применение модуля разности чисел расширяется и зависит от конкретной области знаний или задачи, в которой он используется.
Модуль разности чисел в математических задачах

Модуль разности чисел используется в различных областях математики и занимает важное место в решении задач. Например, в геометрии модуль разности координат двух точек позволяет найти расстояние между ними. В алгебре модуль разности может использоваться для нахождения разницы между двумя значениями или для определения, насколько одно число ближе к нулю, чем другое.
Для нахождения модуля разности чисел следует выполнить следующие шаги:
- Вычислить разность чисел: a - b.
- Взять абсолютное значение полученной разности: |a - b|.
Например, для чисел a = 8 и b = 3:
Делаем вычитание: 8 - 3 = 5.
Берем абсолютное значение разности: |5| = 5.
Итак, модуль разности чисел a и b равен 5.
Таким образом, модуль разности чисел играет важную роль в различных математических задачах, позволяя определить абсолютное значение разности между числами и использовать его для решения задач разных областей математики.
Свойства модуля разности чисел: основные правила

Основные свойства модуля разности чисел:
1. Модуль разности двух чисел всегда неотрицателен. Независимо от того, какое число является большим или меньшим, результат будет всегда положительным числом.
2. Модуль разности двух чисел равен нулю, если эти числа равны. Если вычитаемое и уменьшаемое равны между собой, то результат будет равен нулю.
3. Модуль разности двух чисел равен модулю их суммы, если одно из чисел равно нулю. Если одно из чисел равно нулю (например, вычитаемое), то модуль разности будет равен модулю другого числа (уменьшаемого).
4. Модуль разности двух чисел равен модулю их разности при сохранении знака. Если вычитаемое больше уменьшаемого, то результат будет равен разности этих чисел со знаком минус.
5. Модуль разности двух чисел можно найти, вычитая одно число из другого и затем находя его модуль. Первым шагом нужно найти разность чисел, а затем применить модуль к полученному результату.
Эти основные правила помогут вам правильно применять модуль разности чисел и использовать его в различных математических задачах.
Модуль разности отрицательных чисел: особые случаи

Модуль разности двух чисел представляет собой абсолютное значение их разности. В общем случае, для двух положительных чисел, модуль разности равен значению разности этих чисел.
Однако, при работе с отрицательными числами, возникают особые случаи, которые необходимо учитывать.
- Если разность двух отрицательных чисел положительна, то модуль разности также будет положительным числом.
- Если разность двух отрицательных чисел отрицательна, то модуль разности будет равен абсолютному значению этой разности.
- Если одно из чисел является положительным, а другое отрицательным, то модуль разности всегда будет положительным числом.
Для наглядности, представим несколько примеров:
- Модуль разности чисел -3 и -5 равен 2, так как разность -3 - (-5) = -3 + 5 = 2.
- Модуль разности чисел -7 и -2 равен 5, так как разность -7 - (-2) = -7 + 2 = -5, а модуль от -5 равен 5.
- Модуль разности чисел 4 и -9 равен 13, так как разность 4 - (-9) = 4 + 9 = 13.
Из данных примеров мы видим, что модуль разности отрицательных чисел в некоторых случаях может быть равен положительному числу. Учитывая эти особенности, понимание и правильное использование модуля разности отрицательных чисел становится проще.




