Точки разрыва функции играют важную роль в анализе функций, так как определяют области, в которых функция может иметь особенности, такие как разрывы, перегибы или асимптоты. Найти их помогает понять поведение функции и решить множество математических задач.
Точка разрыва функции обычно появляется, когда функция неопределена или несуществует в некоторой точке. Это может быть связано с различными причинами, такими как деление на ноль, иррациональность, расхождение и др. Но как определить, где именно происходит разрыв? Для этого существует несколько методов и стратегий.
Одним из способов найти точку разрыва функции является анализ ее пределов. Если пределы слева и справа от некоторой точки существуют и равны друг другу, то мы имеем скачок в функции. Если же пределы различны, то возникает разрыв первого рода. В некоторых случаях, пределы могут и не существовать, что означает разрыв бесконечного типа.
Определение точек разрыва функции

Существуют три типа точек разрыва функции: точки разрыва первого рода, в которых функция имеет конечные пределы с обеих сторон, но эти пределы различны; точки разрыва второго рода, в которых хотя бы один из односторонних пределов функции бесконечный; и точки разрыва третьего рода, когда ни один из односторонних пределов функции не существует или бесконечен.
Для определения точек разрыва функции необходимо:
- Найти область определения функции, то есть значения аргумента, при которых функция определена.
- Проверить значения функции в граничных точках области определения.
- Проверить значения функции в точках, где происходят переходы между различными определениями функции, например, точках разрыва дробно-рациональных функций.
- Проверить значения функции в точках, где функция имеет вертикальные или горизонтальные асимптоты.
Обнаружив точку разрыва функции, следует исследовать ее характер: является ли она точкой разрыва первого, второго или третьего рода. Это поможет понять, как функция ведет себя в этой точке и провести соответствующие вычисления при решении задач на определение границ функции.
Пояснение сути и важности понятия

Точки разрыва могут возникать по нескольким причинам. Одна из самых распространенных причин - деление на ноль. Например, функция f(x) = 1/x имеет точку разрыва в x = 0, так как деление на ноль невозможно и функция не определена в этой точке.
Другой причиной может быть наличие разных определений функции в разных интервалах. Например, функция g(x) = |x| имеет точку разрыва в x = 0, так как в левой и правой окрестностях нуля она имеет различные значения (g(x) = -x для x 0).
Понимание точек разрыва функции позволяет анализировать ее поведение и свойства. Например, знание точек разрыва позволяет определить области определения функции, где она непрерывна и может быть проанализирована с использованием методов и инструментов дифференциального и интегрального исчисления.
Важность понятия точек разрыва простирается и на другие области математики и науки. Они играют ключевую роль в теории функций, анализе функций многих переменных и в теории меры и интеграла.
Классификация точек разрыва функции
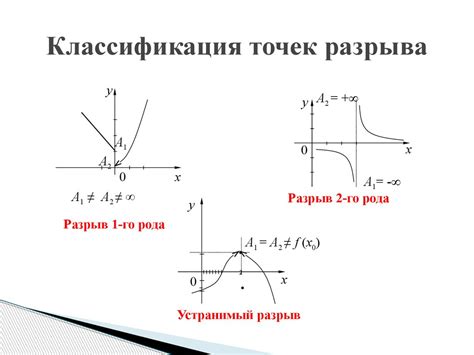
Точки разрыва функции могут быть классифицированы на несколько типов в зависимости от свойств функции в этих точках. Ниже приведены основные типы точек разрыва:
1. Устранимые точки разрыва: В данной точке функция имеет разрыв, но значение функции в этой точке может быть определено путем изменения или "устранения" значения функции в этой точке. Устранимый разрыв происходит, когда значение функции можно определить или исправить. Например, у функции может быть разрыв в точке, где знаменатель равен нулю, но значение функции может быть определено путем упрощения или факторизации.
2. Бесконечные точки разрыва: В данной точке функция имеет разрыв, и значение функции стремится к бесконечности. Бесконечный разрыв происходит, когда знаменатель функции стремится к нулю или функция становится неограниченной в данной точке.
3. Скачок: В данной точке функция имеет разные значения слева и справа от этой точки. Этот тип точки разрыва часто называют "скачком". Скачок может возникнуть из-за различных условий или определений функции по обе стороны точки разрыва. Например, функция может иметь разные значения при x, стремящихся справа и слева к какому-либо числу.
Каждый из этих типов точек разрыва имеет свои особенности и могут быть исследованы с использованием математических методов и анализа функций.
Изучение различных типов разрывов

При изучении точек разрыва функций необходимо учитывать различные типы разрывов, с которыми мы можем столкнуться. В данном разделе рассмотрим несколько основных типов разрывов:
| Тип разрыва | Описание | Пример |
|---|---|---|
| Устранимый разрыв | В данном случае функция имеет разрыв, который можно устранить, определенным образом изменяя значение функции в точке разрыва. | |
| Полюс | Полюс - особый тип разрыва, при котором функция стремится к бесконечности в точке разрыва. | |
| Логический разрыв | Логический разрыв возникает, когда функция не определена в некоторых точках по логическим причинам. | |
| Разрыв первого рода | Разрыв первого рода возникает, когда функция имеет бесконечные значения в точке разрыва, но эти значения не являются полюсом или отсутствующим значением функции. | |
Изучение различных типов разрывов позволит более глубоко понять поведение функций в окрестности точек разрыва и правильно анализировать их свойства.
Как найти точки разрыва функции

Для определения точек разрыва функции нужно проверить следующие условия:
- Особые значения: Проверить, есть ли значения функции, при которых функция не определена или не существует предел в этой точке. Такие точки могут возникать из-за деления на ноль, извлечения корня из отрицательного числа и других операций, которые не имеют смысла в математике.
- Устранимые разрывы: Проверить, существуют ли у функции устранимые разрывы, когда два одинаковых предела конечны, но не равны друг другу. Такие разрывы могут возникать, например, из-за наличия асимптоты у функции.
- Бесконечные разрывы: Проверить, существуют ли у функции бесконечные разрывы, когда хотя бы один из пределов является бесконечным. Такие разрывы могут возникать, например, из-за деления на ноль или приближения к бесконечности по аргументу функции.
- Разные пределы: Проверить, существуют ли у функции разные пределы при приближении к точке с разных сторон. Такие разрывы могут возникать, например, при наличии различных асимптот у функции.
После выполнения этих проверок можно сделать вывод о наличии или отсутствии точек разрыва функции и определить их тип. Найденные точки разрыва могут помочь понять особенности функции и поведение графика в этих точках.
Например, рассмотрим функцию f(x) = 1 / x. В этой функции возникает точка разрыва при x = 0 из-за деления на ноль. Также функция имеет бесконечный разрыв при x = 0, так как предел функции при приближении к нулю равен бесконечности. Точка разрыва при x = 0 является точкой разрыва второго рода.
Практические способы определения точек разрыва
Для нахождения точек разрыва функции можно использовать различные методы и инструменты. Рассмотрим несколько из них:
1. Аналитический метод
Этот метод предполагает анализ аналитической формы функции и ее параметров. Точки разрыва могут возникать при изменении знака выражения в знаменателе функции, а также при наличии разрыва в определении функции (например, при делении на ноль).
Для определения точек разрыва сначала анализируется знаменатель функции, и находятся значения переменных, при которых он равен нулю. Затем проверяется, возникает ли у функции разрыв при данных значениях, путем анализа числителя функции и подстановки найденных значений в знаменатель.
2. Графический метод
Для определения точек разрыва можно построить график функции. Точки разрыва будут представлять собой места, где график функции имеет разрыв или разрывы. Графический метод является визуальным и может быть полезным в случае, когда аналитический метод сложно применить или не дает однозначного результата.
При построении графика функции следует обратить внимание на особенности поведения функции вблизи потенциальных точек разрыва, таких как разрывы первого рода (разрывы с переходом лимита функции в бесконечность или в минус бесконечность) и разрывы второго рода (разрывы, когда лимит функции не существует).
3. Вычислительный метод
При использовании вычислительного метода точки разрыва находятся численно, с помощью компьютерных программ или онлайн-калькуляторов, которые могут вычислить значения функции в заданных точках и показать наличие разрыва.
Вычислительный метод особенно полезен в случае сложных функций или большого количества переменных, когда аналитический анализ затруднен или невозможен.
Важно помнить, что определение точек разрыва функции требует тщательного анализа и исследования функции. Результаты, полученные при использовании различных методов, следует сравнивать и проверять другими способами, чтобы достичь достоверности и точности.




