Вычисление значений дробей – один из важных навыков в математике, который поможет вам решать широкий спектр задач и применять его в повседневной жизни. В этой статье мы рассмотрим простые способы и подробно объясним, как найти значение выражения дроби.
Первым шагом в вычислении значений дробей является определение числителя и знаменателя. Числитель – это число, расположенное над чертой дроби, а знаменатель – число, находящееся под чертой. Например, в дроби 3/4 числитель равен 3, а знаменатель равен 4.
Для вычисления значения дроби необходимо выполнить простые арифметические операции. Если числитель и знаменатель являются целыми числами, то значение дроби можно найти, разделив числитель на знаменатель. Например, дробь 3/4 равна 3 делить на 4, что равно 0.75.
Однако, в некоторых случаях числитель или знаменатель могут быть десятичными числами или иметь переменные. В таких случаях необходимо выполнить определенные алгоритмы для нахождения значения дроби.
В следующих разделах статьи мы рассмотрим конкретные примеры и пошагово объясним, как найти значение выражения дроби с различными числами и переменными.
Как вычислить значение дроби: подробное объяснение и простые способы
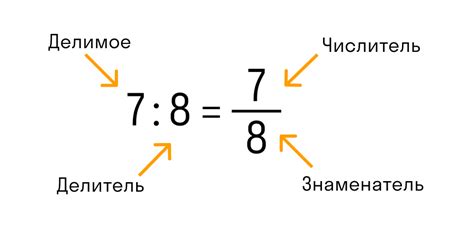
Десятичная форма
Воспользуемся простым способом вычисления значения дроби - переводом ее в десятичную форму. Для этого достаточно разделить числитель на знаменатель. Например, чтобы найти значение дроби 3/4, нужно выполнить следующую операцию:
| 3 |
| ÷ |
| 4 |
Результатом деления будет число 0,75. Таким образом, значение дроби 3/4 равно 0,75.
Процентная форма
Еще одним простым способом вычисления значения дроби является перевод ее в процентную форму. Для этого числитель необходимо разделить на знаменатель, умножить на 100 и добавить знак процента (%). Например, чтобы найти значение дроби 2/5, нужно выполнить следующую операцию:
| 2 |
| ÷ |
| 5 |
| = |
| 0,4 |
| × |
| 100 |
| = |
| 40% |
Таким образом, значение дроби 2/5 равно 40%.
В данной статье мы рассмотрели простые способы вычисления значения дроби: десятичную и процентную формы. Они позволяют получить численный результат без дополнительных вычислений. Следует отметить, что существуют и другие методы вычисления дробей, однако они требуют более сложных математических операций.
Что такое дробь и как вычислить ее значение?
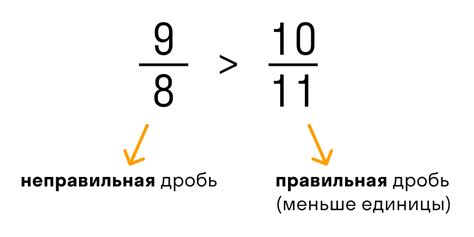
Чтобы вычислить значение дроби, необходимо разделить числитель на знаменатель. Например, если у нас есть дробь 3/4, то значение этой дроби можно найти, разделив числитель 3 на знаменатель 4. В результате получится число 0,75, что означает, что дробь 3/4 является долей от целого числа, равной 0,75.
Если числитель и знаменатель дроби имеют общие делители, то перед делением их нужно сократить. Например, дробь 6/8 можно сократить, разделив числитель и знаменатель на их общий делитель 2. В результате получится дробь 3/4 с тем же значением, но в упрощенной форме.
Для более сложных дробей, включающих десятичные доли или периодические десятичные числа, существуют специальные правила вычисления, которые требуют более подробного объяснения. Однако в общем случае, вычисление значения дроби сводится к простому делению числителя на знаменатель.
| Числитель | Знаменатель | Значение |
|---|---|---|
| 3 | 4 | 0,75 |
| 6 | 8 | 0,75 |
Простой способ вычислить значение дроби с одинаковыми знаменателем и числителем

Для вычисления значения дроби, у которой числитель и знаменатель равны (например, 3/3 или 5/5), достаточно простого действия. Из-за того, что числитель и знаменатель имеют одно и то же значение, результат всегда будет равен 1.
Дробь с одинаковыми числителем и знаменателем может быть записана как:
| Числитель | Знаменатель | Значение |
|---|---|---|
| 3 | 3 | 1 |
| 5 | 5 | 1 |
| 7 | 7 | 1 |
Таким образом, если числитель и знаменатель дроби равны, ответ всегда будет одним и тем же числом - 1. Это очень простой способ решения таких дробных выражений.
Как вычислить значение дроби с разными знаменателем и числителем

Вычисление значения дроби с разными знаменателем и числителем возможно при условии выполнения следующих шагов:
1. Найдите наименьшее общее кратное (НОК) знаменателей дробей. Для этого можно воспользоваться разложением знаменателей на простые множители и выбрать их наибольшие степени.
2. Приведите обе дроби к общему знаменателю, умножив числители и знаменатели на соответствующие множители. Таким образом, вам будет дана пара эквивалентных дробей с одинаковым знаменателем.
3. Сложите (или вычтите) числители получившихся дробей и запишите результат. Знаменатель останется неизменным.
4. Приведите результат к наиболее простому виду, если это необходимо. Например, сократите дробь, если числитель и знаменатель имеют общие делители.
Таким образом, с помощью этих шагов можно вычислить значение дроби с разными знаменателем и числителем в более подробной форме.




