В математике существует понятие нулей функции, которые представляют собой значения аргументов, при которых функция равна нулю. Но что означает отсутствие нулей функции? Как понять, что функция не обращается в ноль ни при каких значениях аргументов?
Отсутствие нулей функции означает, что не существует таких значений аргументов, при которых функция равна нулю. Другими словами, график функции не пересекает ось OX и не имеет точек, где Y-координата равна нулю. Такое свойство функции может быть важным при решении различных задач: от определения области применения функции до анализа ее поведения.
Чтобы понять, что функция не имеет нулей, можно воспользоваться графиком, уравнением функции или ее аналитическими свойствами. Если график функции лежит полностью выше или ниже оси OX, то это означает, что функция не пересекает эту ось и, следовательно, не имеет нулей. Уравнение функции также может дать информацию о наличии или отсутствии нулей. Если при решении уравнения не удается найти значения аргументов, при которых функция равна нулю, то функция не имеет нулей.
Отсутствие нулей функции может свидетельствовать о том, что она монотонна и не меняет знак на всей области определения. Это может быть полезным свойством при анализе функции и решении различных задач.
Что значит "нет нулей функции"
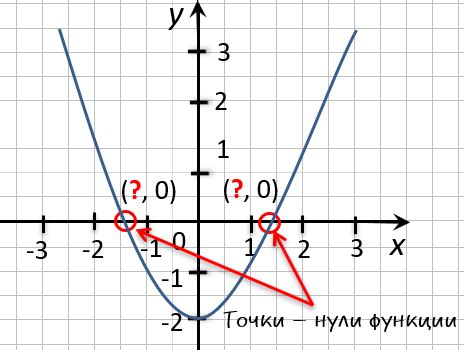
В математике понятие "нет нулей функции" означает отсутствие таких значений аргумента, при которых функция равна нулю. То есть, функция не пересекает ось абсцисс и не имеет точек, где её значение равно нулю.
Если функция не имеет нулевых значений, то график функции не пересекает ось абсцисс. Это может означать, что функция всегда положительна или всегда отрицательна, в зависимости от её характера.
Нет нулей функции можно определить, анализируя её алгебраическую формулу или график. Например, если функция представлена в виде квадратного уравнения, то её нули можно найти, решив это уравнение. Если решением уравнения являются только комплексные числа или уравнение не имеет решений, то функция не имеет нулей.
Отсутствие нулей функции может быть полезным понятием в различных математических и научных областях. Например, при исследовании свойств функций или при решении уравнений и систем уравнений может потребоваться определить, имеет ли функция нули или нет.
Определение понятия "нет нулей функции"

В математике понятие "нет нулей функции" означает, что функция не принимает значения 0 на всем своем области определения. Иными словами, нет таких значений аргумента, при которых функция равна нулю.
Это понятие имеет важное значение в анализе функций и исследовании их свойств. Если у функции нет нулей, это может указывать на ее монотонность или наличие периода без изменения знака. Например, положительная функция без нулей может означать, что она всегда принимает положительные значения, а отрицательная функция без нулей – что она всегда отрицательна.
Проверить наличие или отсутствие нулей функции можно, решив уравнение f(x) = 0. Если такое уравнение не имеет решений, то нет нулей функции.
Определение отсутствия нулей функции является важным инструментом для аналитического исследования функций и нахождения их основных свойств. Понимая, что у функции нет нулей, мы можем делать выводы о ее поведении, форме графика и других характеристиках.
Почему это важно

Понимание отсутствия нулей функции играет важную роль в различных областях математики и естественных наук. Нет нулей функции означает, что функция не пересекает ось абсцисс и не принимает значение 0 на всем своем домене. Это имеет прямое влияние на свойства и поведение функции.
Одним из основных применений знания о нет нулей функции является разрешение уравнений и систем уравнений. Зная, что функция не имеет нулей, можно сделать вывод о том, что решений для уравнения не существует или они находятся за пределами заданного диапазона. Это позволяет сократить время и усилия при решении математических и инженерных задач.
В физике отсутствие нулей функции также имеет важное значение. Например, когда мы изучаем движение тела, функция, описывающая зависимость пути от времени, не должна иметь нулей, так как это указывает на моменты, когда тело остановилось или сместилось в обратном направлении.
Безопасность также является одним из факторов, где понимание нет нулей функции может сыграть важную роль. Например, в области информационной безопасности или защиты данных, функции, которые должны быть невозможными для вычисления в нуле, требуют уточнения и обеспечения отсутствия нулей. Это помогает предотвратить взлом, обнаружение и понижение защищенности системы.
И, наконец, понимание концепции нет нулей функции помогает углубить знания о функциях в целом и провести более сложные исследования. Отсутствие нулей может указывать на наличие симметрии или особенных свойств функции, что может быть дополнительной информацией при анализе и построении графиков функций.
Как понять, что функция не имеет нулей
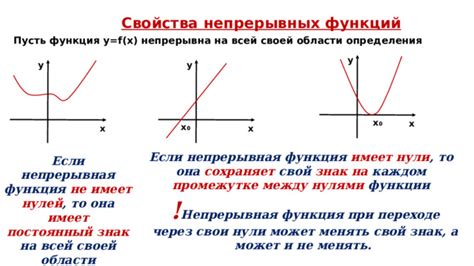
Следующие методы могут помочь вам понять, имеет ли функция нули:
- Если функция представлена графически, просмотрите ее график. Если на графике не существует точек, в которых график пересекает ось x (горизонтальную ось), то функция не имеет нулей.
- Можно также использовать аналитический подход, решая уравнение функции f(x) = 0. Если уравнение не имеет решений или существует только фиктивное значение x, то функция не имеет нулей.
- Если функция задана в виде алгебраического выражения, можно проанализировать ее свойства и применить теоремы, связанные с нулями функции. Например, если функция квадратичная, можно использовать формулу дискриминанта для определения количества нулей.
- Если функция задана в табличной форме, вы можете осуществить перебор всех значений x и проверить, существуют ли такие значения, при которых f(x) = 0.
Важно отметить, что отсутствие нулей в функции не означает, что она не имеет других интересных свойств или не может быть полезной в контексте других проблем. Нуль функции – это лишь один из ее аспектов, и несуществование нулей не делает функцию менее важной или интересной.
Примеры функций без нулей
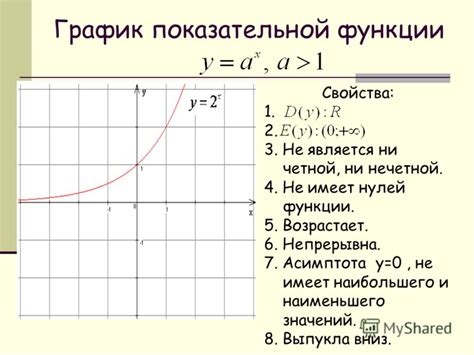
В математике существуют множество функций, которые не имеют нулей. Это означает, что значение функции никогда не достигает нуля при любых значениях независимой переменной.
Ниже приведены несколько примеров функций, которые не имеют нулей:
- Константная функция: f(x) = c, где с - постоянное число. Независимо от значения переменной x, функция всегда будет равна постоянному числу c.
- Экспоненциальная функция: f(x) = a^x, где a - положительное число, отличное от 1. Эта функция всегда положительна и никогда не равна нулю.
- Логарифмическая функция: f(x) = log_a(x), где a - положительное число, отличное от 1. Значение функции всегда будет положительным и никогда не равным нулю.
- Тригонометрическая функция: f(x) = sin(x). Значение синуса никогда не достигает нуля при любых значениях угла x.
Это всего лишь несколько примеров функций без нулей. Существует и другие функции, которые также не имеют нулей. Понимание этого понятия важно при изучении математики и анализе функций.
Выводы

Отсутствие нулей функции означает, что график функции не пересекает ось абсцисс. Это может иметь различные практические интерпретации в зависимости от контекста задачи.
Нет нулей функции может означать, что в заданной области определения функции нет точек, где она обращается в ноль. В таких случаях функция полностью содержится либо выше, либо ниже оси абсцисс.
Это свойство функции может быть важным при решении задач уравнений и неравенств, а также при определении положения графика функции относительно оси абсцисс.
Обратите внимание, что наличие или отсутствие нулей функции не всегда является прямым свидетельством о ее поведении. Некоторые функции могут иметь разные графики, несмотря на отсутствие нулей.
В целом, отсутствие нулей функции является важным свойством, которое может помочь нам лучше понять ее поведение и свойства.




