Коммутация матрицы - это одна из основных операций в линейной алгебре, которая имеет важное значение во многих областях, включая физику, компьютерную графику и криптографию. В этой операции две матрицы перемножаются в порядке, обратном их расположению, и результат операции называется коммутированной матрицей.
Для коммутации матрицы необходимо, чтобы размерности матриц позволяли выполнить операцию умножения. Важно отметить, что коммутативность матриц не является обязательным свойством. То есть, в общем случае AB ≠ BA, где A и B - матрицы. Поэтому коммутированная матрица может иметь совершенно другой вид и свойства, чем исходные матрицы A и B.
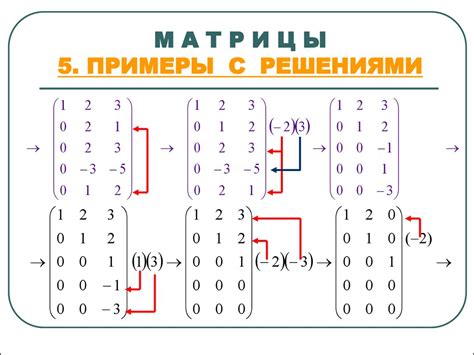
Пример:
Рассмотрим две матрицы:
A = [1 2]
[3 4]
B = [5 6]
[7 8]
Вычисляем произведение матриц, в порядке, обратном их расположению:
BA = [23 34]
[31 46]
AB = [19 34]
[43 62]
Таким образом, коммутированная матрица для данного примера будет:
[23 34]
[31 46]
Как видно из примера, результат операции коммутации матриц зависит от исходных матриц A и B и порядка их расположения.
Что такое матричная коммутация и как ее применять: общее понятие
Для двух матриц А и В процесс коммутации записывается как [А, В] и определяется следующим образом:
- Если А и В являются скалярными величинами (т.е. одномерными массивами), то [А, В] равно нулю, так как порядок умножения скаляров не имеет значения.
- Если А и В являются двумерными матрицами одинаковой размерности, то [А, В] будет равно А*В - В*А, где * обозначает матричное умножение.
- Если А и В имеют различный размер или одна из матриц является вектором, то коммутация невозможна и [А, В] будет равно нулю.
Матричная коммутация имеет множество приложений в различных областях математики и физики. Например, она может использоваться для упрощения выражений, анализа симметрий или решения уравнений в частных производных. Также коммутация имеет важное значение в теории групп и квантовой механике.
Давайте рассмотрим пример применения матричной коммутации:
Пусть у нас есть две матрицы:
А = [[1, 2], [3, 4]]
В = [[5, 6], [7, 8]]
Применим коммутацию:
[А, В] = А*В - B*A
= [[1, 2], [3, 4]] * [[5, 6], [7, 8]] - [[5, 6], [7, 8]] * [[1, 2], [3, 4]]
= [[19, 22], [43, 50]] - [[23, 34], [31, 46]]
= [[-4, -12], [12, 16]]
Полученная матрица является результатом матричной коммутации и может быть использована для дальнейших вычислений или анализа.
Определение матричной коммутации
Для двух квадратных матриц A и B их коммутатором называется матрица, получаемая вычитанием произведения A и B из произведения B и A:
[A, B] = AB - BA
Если полученная матрица коммутатора равна нулевой матрице, то говорят, что матрицы A и B коммутируют.
Коммутация матриц имеет важное значение в физике, особенно в квантовой механике, где операторы часто представляются в матричной форме. Поиск коммутатора операторов позволяет определить, коммутируют ли они и, следовательно, могут ли быть измерены одновременно.
Примеры использования коммутирования матриц
Коммутирование матриц имеет широкое применение в различных областях, связанных с линейной алгеброй и теорией графов. Вот несколько примеров, чтобы лучше понять, как работает коммутирование матриц:
Криптография: коммутирование матриц используется для шифрования и дешифрования сообщений. Например, в шифре Хилла матрицы используются для перекодирования отдельных символов, и коммутирование матриц позволяет повысить безопасность шифрования.
Машинное обучение: в алгоритмах машинного обучения, связанных с матричными операциями, коммутирование матриц используется для оптимизации процесса вычислений и ускорения работы алгоритма.
Теория графов: коммутирование матриц позволяет рассматривать свойства и связи между различными графами. Например, используя коммутирование матриц, можно определить, являются ли два графа изоморфными или эквивалентными.
Системы управления: коммутирование матриц используется для анализа и моделирования различных систем управления, таких как электрические цепи, робототехника и др. Это помогает оптимизировать и предсказывать поведение системы в различных ситуациях.
Это лишь некоторые примеры использования коммутирования матриц. В действительности, коммутирование матриц является одной из фундаментальных операций линейной алгебры и имеет множество применений в различных областях науки и техники.
Преимущества и области применения коммутирования матриц

Преимущества коммутирования матриц включают:
- Упрощение вычислений: коммутирование матриц позволяет сократить количество операций при выполнении линейных вычислений.
- Повышение эффективности: использование коммутирования матриц позволяет улучшить производительность алгоритмов и программ, особенно при работе с большими объемами данных.
- Улучшение устойчивости: коммутирование матриц может помочь снизить погрешность вычислений, улучшить устойчивость алгоритмов и предотвратить ошибки округления.
- Удобство в использовании: коммутирование матриц позволяет удобно записывать и представлять сложные операции, что делает их более понятными и легко читаемыми.
Области применения коммутирования матриц включают следующие:
- Криптография: коммутирование матриц широко применяется при шифровании и дешифровании информации. Оно обеспечивает безопасность передачи данных и предотвращает возможность подделки или взлома.
- Теория графов: коммутирование матриц используется при анализе и моделировании связей и взаимодействий в графах. Оно помогает решать задачи, связанные с оптимизацией и поиском путей.
- Машинное обучение: коммутирование матриц находит применение в обработке и анализе данных, классификации и кластеризации, а также в направленных алгоритмах обучения.
- Физика и наука о материалах: коммутирование матриц используется при моделировании и анализе различных физических и материальных систем, включая электрические цепи, квантовую механику и оптику.
Коммутирование матриц играет важную роль в многих областях знания и науки, и его применение продолжает расширяться по мере развития новых технологий и методов.




