Кратчайший маршрут - это наиболее выгодный и быстрый путь от одного места к другому. Он может быть определен разными способами, в зависимости от конкретной ситуации и требований.
Поиск кратчайшего маршрута играет важную роль в различных сферах человеческой деятельности, таких как транспорт, логистика, планирование маршрутов и другие. Он позволяет экономить время, ресурсы и снижать издержки.
Принципы поиска кратчайшего маршрута основаны на алгоритмах, которые позволяют находить оптимальные пути. Одним из самых популярных и широко используемых алгоритмов является алгоритм Дейкстры. Он основан на поиске кратчайших путей от начальной точки до всех остальных точек графа.
Алгоритм Дейкстры работает постепенно расширяя достигнутые вершины, находя и запоминая самые короткие пути до каждой из них.
Кроме алгоритма Дейкстры, существует множество других алгоритмов для поиска кратчайших маршрутов, таких как алгоритм Флойда-Уоршелла, алгоритм A*, алгоритмы волнового типа и многие другие. Каждый из них имеет свои преимущества и недостатки, и выбор определенного алгоритма зависит от конкретной задачи и условий ее решения.
Что такое кратчайший маршрут и как его найти?

Для нахождения кратчайшего маршрута существуют различные алгоритмы, которые позволяют эффективно решать данную задачу:
- Алгоритм Дейкстры – один из наиболее популярных алгоритмов поиска кратчайшего маршрута. Он основывается на принципе поиска от точки начала к конечной точке, попутно обновляя длину пути до соседних точек. Алгоритм Дейкстры гарантирует нахождение кратчайшего пути, но может быть неэффективным для графов с большим числом вершин.
- Алгоритм Флойда-Уоршелла – алгоритм, который позволяет находить кратчайший путь между всеми парами вершин в графе. Он основывается на построении таблицы расстояний между всеми парами вершин и обновлении этой таблицы на каждой итерации. Алгоритм Флойда-Уоршелла может быть эффективен для небольших графов, но может стать неэффективным при большом количестве вершин.
- Алгоритм A* – эффективный алгоритм поиска кратчайшего пути в графе, основывающийся на эвристической оценке расстояния до конечной точки. Он комбинирует принципы алгоритма Дейкстры с эвристической функцией для выбора наиболее оптимального пути. Алгоритм A* часто используется в играх, робототехнике и других областях, где требуется быстрый поиск кратчайшего пути.
Кратчайший маршрут является важной задачей в многих областях, и его нахождение может существенно улучшить процессы и экономить время и ресурсы. Выбор конкретного алгоритма зависит от особенностей задачи и требований к эффективности и точности решения.
| Определение и особенности поиска кратчайшего маршрута |
|---|
Поиск кратчайшего маршрута может быть осуществлен с помощью различных алгоритмов, таких как алгоритм Дейкстры или алгоритм A*. Основная задача состоит в нахождении оптимального пути, удовлетворяющего определенным критериям, например, минимальной стоимости или самого короткого расстояния. Особенностью поиска кратчайшего маршрута является то, что он может быть применен к различным типам графов: направленным или ненаправленным, взвешенным или невзвешенным. Также он может учитывать различные ограничения, такие как преграды, перекрестки или дорожные правила. Кроме того, поиск кратчайшего маршрута может быть решен как задача одиночного пути, когда требуется найти оптимальный путь между двумя заданными точками, или задача нахождения всех кратчайших путей, когда требуется найти все возможные оптимальные пути между всеми узлами графа. |
Принципы поиска кратчайшего маршрута
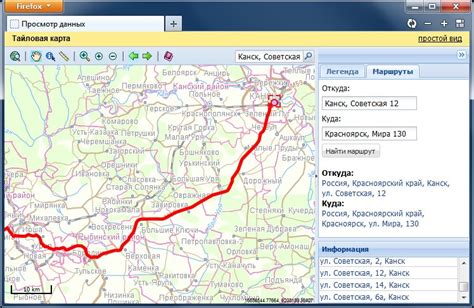
1. Алгоритмы поиска
Для поиска кратчайшего маршрута в графовых структурах существует несколько алгоритмов. Один из наиболее распространенных алгоритмов – это алгоритм Дейкстры. Он основан на пошаговом просмотре вершин графа, от начальной до конечной, с обновлением самого короткого пути на текущий шаг. Еще один часто используемый алгоритм – это алгоритм А* (A-star). Он комбинирует эвристическую функцию для оценки расстояния до цели и информацию о предыдущих пройденных участках пути. Это помогает ускорить процесс поиска кратчайшего маршрута.
2. Определение веса ребер
Для поиска кратчайшего маршрута важно определить вес каждого ребра в графе. В зависимости от конкретной задачи, вес ребра может быть определен либо как физическое расстояние, либо как время или затраты, необходимые для преодоления данного участка пути. Некоторые алгоритмы учитывают и другие факторы, такие как пропускная способность или стоимость проезда.
3. Учет ограничений
При поиске кратчайшего маршрута может потребоваться учет различных ограничений и ограничительных факторов. Например, маршрут может быть ограничен по времени, по наличию определенных объектов или по типу дороги. Алгоритмы поиска должны учитывать эти ограничения при построении маршрута.
4. Учет динамических изменений
Реальные условия на дорогах и других маршрутах могут меняться со временем. Это может включать пробки, аварии или временные ограничения. Поэтому важно иметь возможность учитывать динамические изменения при поиске кратчайшего маршрута. Для этого алгоритмы могут использовать актуальные данные о трафике или осуществлять обновление маршрута в режиме реального времени.
При поиске кратчайшего маршрута необходимо учитывать не только длину пути, но и другие факторы, такие как время, допустимые ограничения и изменяющиеся условия. Это позволяет найти оптимальный маршрут, удовлетворяющий требованиям пользователя или задаче.




