Нормирование данных – это процесс приведения значений переменных к определенным диапазонам или шкалам. Цель нормализации данных состоит в улучшении процесса анализа и моделирования данных, увеличении эффективности алгоритмов машинного обучения и их интерпретируемости.
Основная причина, по которой данные нормируются, заключается в том, что переменные в наборе данных могут быть измерены в различных масштабах, иметь разные диапазоны значений и единицы измерения. Несбалансированные переменные могут привести к нежелательным эффектам при работе с моделями машинного обучения, таким как градиентный спуск, который может уйти в бесконечность или слишком сильно зависеть от одной переменной.
Методы нормализации данных
Существует несколько основных методов нормализации данных. Один из самых распространенных методов – это стандартизация. При стандартизации данные приводятся к распределению с нулевым средним и стандартным отклонением равным единице. Этот метод особенно полезен в задачах, где требуется сравнение различных переменных, потому что он выбирает довольно универсальный масштаб.
Другой метод нормализации данных – это минимаксная нормализация. При этом методе данные приводятся к диапазону от 0 до 1. Для каждого значения переменной вычисляется отношение к разнице между максимальным и минимальным значениями переменной. Данный метод часто используется, если существуют очень большие различия в значениях переменных или при работе с алгоритмами, которые более эффективно работают с данными в таком диапазоне.
Значение нормирования данных

Нормализация данных является одним из ключевых шагов в предварительной обработке данных. Она может осуществляться различными методами, в зависимости от характеристик данных и поставленных задач. Результатом нормализации являются пересчитанные значения, которые обеспечивают понимание данных в более подходящем формате.
Основная цель нормализации данных - улучшить работу алгоритмов машинного обучения путем снижения влияния различных единиц измерения и масштабов переменных на результаты моделирования. Это позволяет более точно интерпретировать результаты и делать более обоснованные выводы.
Нормализация данных также может помочь предотвратить проблемы, связанные с выбросами. В случае наличия аномальных значений, не нормализованные данные могут существенно искажать результаты анализа и приводить к неправильным выводам. После нормализации выбросы становятся менее значимыми и могут быть правильно обработаны.
Важно отметить, что нормализация данных необходима не для всех алгоритмов и задач. Некоторые алгоритмы, такие как деревья решений или алгоритмы на основе правил, не требуют нормализации данных, поскольку они не зависят от масштаба переменных. Однако, в большинстве случаев нормализация полезна и даже необходима для успешного анализа данных и моделирования.
Методы нормализации данных
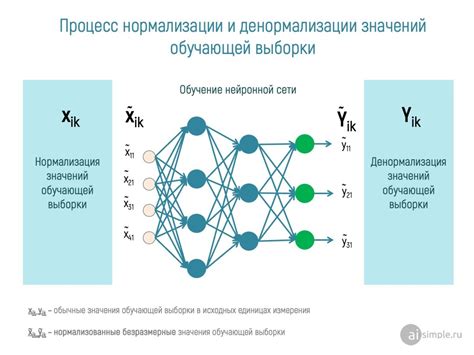
Существует несколько основных методов нормализации данных, которые могут быть применены в зависимости от характеристик и требований данных:
1. Диапазонная нормализация
Метод диапазонной нормализации, также известный как минимаксное масштабирование или приведение к интервалу, преобразует значения переменных таким образом, чтобы они находились в заданном диапазоне, чаще всего от 0 до 1 или от -1 до 1. Простейшая формула для диапазонной нормализации:
X_new = (X - X_min) / (X_max - X_min)
Где X_new - нормализованное значение, X - исходное значение переменной, X_min - минимальное значение переменной, X_max - максимальное значение переменной.
2. Стандартизация
Стандартизация, также известная как Z-нормализация или Z-преобразование, преобразует значения переменных таким образом, чтобы они имели среднее значение 0 и стандартное отклонение 1. Формула для стандартизации:
X_new = (X - X_mean) / X_std
Где X_new - стандартизированное значение, X - исходное значение переменной, X_mean - среднее значение переменной, X_std - стандартное отклонение переменной.
3. Логарифмическая нормализация
Логарифмическая нормализация используется для изменения распределения переменной и уменьшения размаха значений. Логарифмическая нормализация применяется к положительным значениям переменных с помощью логарифмической функции. Формула для логарифмической нормализации:
X_new = log(X + 1)
Где X_new - нормализованное значение, X - исходное значение переменной.
Это не все методы нормализации, которые могут быть использованы при работе с данными, но они являются одними из самых распространенных и простых в использовании. Выбор метода нормализации зависит от типа данных, характеристик и целей исследования.
Стандартизация

Для стандартизации признаков используется формула:
X_std = (X - X.mean()) / X.std()
Где:
X_std - стандартизованное значение признака;
X - исходное значение признака;
X.mean() - среднее значение признака;
X.std() - стандартное отклонение признака.
Стандартизация полезна в случаях, когда значения признаков имеют различный масштаб и единицы измерения. Она также может быть полезной для алгоритмов машинного обучения, которые зависят от масштаба данных.
Пример применения стандартизации: если у нас есть данные о зарплатах, где значения варьируются от 20 000 до 100 000, а также данные об опыте работы, где значения варьируются от 1 до 50, то эти признаки имеют разный масштаб и единицы измерения. Стандартизацией мы приведем оба признака к общему виду, чтобы они стали более сравнимыми.
Мин-Макс нормализация

Мин-Макс нормализация основана на следующей формуле:
X_norm = (X - X_min) / (X_max - X_min)
Где:
- X_norm - это нормализованное значение переменной
- X - это исходное значение переменной
- X_min - это минимальное значение переменной
- X_max - это максимальное значение переменной
Процесс мин-макс нормализации состоит из двух этапов:
- Нахождение минимального и максимального значения переменной.
- Применение формулы для каждого значения переменной.
Пример:
Допустим, у нас есть следующий набор данных: [10, 20, 30, 40, 50].
На первом этапе мы находим минимальное значение (10) и максимальное значение (50).
На втором этапе мы используем формулу мин-макс нормализации для каждого значения:
- X1_norm = (10 - 10) / (50 - 10) = 0
- X2_norm = (20 - 10) / (50 - 10) = 0.1
- X3_norm = (30 - 10) / (50 - 10) = 0.2
- X4_norm = (40 - 10) / (50 - 10) = 0.3
- X5_norm = (50 - 10) / (50 - 10) = 0.4
Теперь значения переменной находятся в диапазоне от 0 до 1.
Мин-Макс нормализация широко используется в машинном обучении и статистике, особенно при работе с алгоритмами, которые требуют масштабирования данных, такими как нейронные сети и методы, основанные на евклидовом расстоянии.
Средневзвешенная нормализация
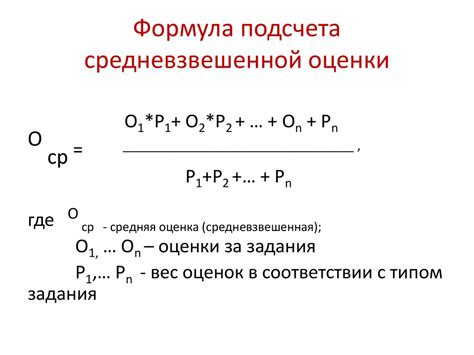
Основная идея средневзвешенной нормализации заключается в том, чтобы присвоить различные значения переменным в зависимости от их важности. Каждая переменная умножается на соответствующий ей вес, а затем значения суммируются и делятся на суммарный вес. Таким образом, значения переменных получаются взвешенными, что позволяет учитывать их вклад в общий результат.
Процесс средневзвешенной нормализации можно описать следующим образом:
- Установить веса для каждой переменной. Веса могут быть присвоены вручную на основе экспертных оценок или вычислены с использованием различных методов, таких как методы машинного обучения.
- Умножить каждое значение переменной на соответствующий ей вес.
- Суммировать взвешенные значения всех переменных.
- Поделить полученную сумму на суммарный вес.
Результатом средневзвешенной нормализации является набор значений переменных, приведенных к относительной шкале от 0 до 1. Это позволяет сравнивать значения разных переменных и учитывать их важность при анализе данных или принятии решений.
Средневзвешенная нормализация широко используется в различных областях, включая экономику, финансы, маркетинг и технические науки. Этот метод позволяет эффективно сравнивать и анализировать данные, учитывая их взаимное влияние и важность.
Подробное объяснение нормализации данных
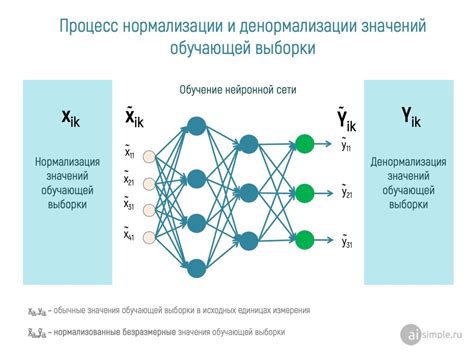
Когда данные содержат разные значения в разных единицах измерения или имеют большой разброс, это может привести к проблемам при их интерпретации и использовании. Это особенно важно для алгоритмов машинного обучения, которые требуют численных данных в определенном диапазоне для эффективного функционирования. Нормализация данных позволяет привести данные к единому масштабу, что помогает избежать этих проблем.
Основные методы нормализации данных включают следующие:
- Масштабирование данных - метод, который масштабирует значения данных в определенном диапазоне. Наиболее распространенным способом масштабирования данных является метод минимакс, который масштабирует значения данных в интервале от 0 до 1.
- Стандартизация данных - метод, который приводит значения данных к нулевому среднему и единичному стандартному отклонению. Стандартизация данных полезна в случае, когда данные имеют разные единицы измерения или различаются их распределения.
- Нормализация Z-оценки (Z-нормализация) - метод, который приводит значения данных к нулевому среднему и единичному стандартному отклонению, используя формулу Z-оценки. Данный метод полезен при работе с данными, которые имеют нормальное распределение.
- Логарифмическая трансформация - метод, который применяет логарифмическую функцию к значениям данных. Логарифмическая трансформация полезна в случае, когда данные имеют асимметричное или экспоненциальное распределение.
Выбор конкретного метода нормализации данных зависит от типа данных и их распределения. Важно осознавать, что нормализация данных может повлиять на результаты анализа данных и принятие решений, поэтому выбор метода должен быть обдуманным и основываться на анализе самих данных.
В целом, нормализация данных является неотъемлемой частью процесса обработки данных и является важным шагом перед использованием данных в анализе и алгоритмах машинного обучения. Правильное применение методов нормализации данных помогает упростить анализ данных и повышает эффективность алгоритмов машинного обучения во многих областях, от финансов до медицины.




