Что значит абсцисса вектора

Абсцисса вектора является одним из важных понятий в линейной алгебре. Она представляет собой координату точки на числовой оси, от которой отсчитывается вектор. Абсцисса позволяет определить положение вектора относительно начала координат и играет важную роль в решении различных задач, связанных с векторами.

Определение абсциссы вектора основывается на понятии координаты. Координаты вектора представляют собой числа, определяющие его положение на плоскости или в пространстве. Абсцисса является одной из координат и обычно обозначается буквой "x".

Свойства абсциссы вектора включают возможность определения его направления и длины. Кроме того, абсцисса позволяет выполнять операции с векторами, такие как сложение и вычитание, а также умножение на скаляр.

Примеры использования абсциссы вектора можно найти в различных областях, включая математику, физику, графику и программирование. Например, при решении задач динамики материальной точки абсцисса может использоваться для определения перемещения точки в пространстве. В графике абсцисса позволяет определить положение точки на плоскости и построить график функции. В программировании абсцисса может использоваться для определения положения объекта на экране или в пространстве.

Определение абсциссы

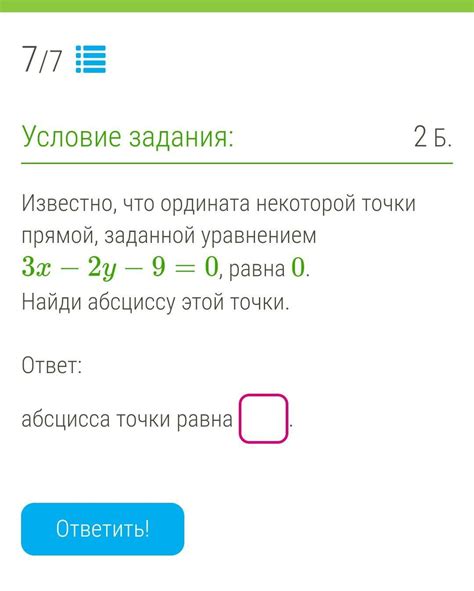
Абсцисса вектора обозначается символом x. Для вектора a абсциссу обозначают как x_a.

Значение абсциссы может быть положительным, отрицательным или равным нулю, в зависимости от положения точки, которая является концом вектора, относительно начала координат.

Определение абсциссы позволяет нам точно определить положение вектора на оси абсцисс и использовать его в дальнейших математических операциях и вычислениях.

Свойства абсциссы вектора

Вот несколько свойств абсциссы вектора:

Сложение: Абсцисса суммы двух векторов равна сумме абсцисс этих векторов.
Умножение на скаляр: Умножение абсциссы вектора на скаляр равно умножению этого скаляра на абсциссу вектора.
Противоположный вектор: Абсцисса противоположного вектора равна минус абсциссе исходного вектора.
Нулевой вектор: Абсцисса нулевого вектора равна нулю.

Например, если у нас есть вектор с абсциссой 3, то сумма этого вектора с вектором абсциссой 2 будет иметь абсциссу 5 (3 + 2). Умножение вектора с абсциссой 3 на скаляр 4 даст вектор с абсциссой 12 (3 * 4). Противоположный вектор к вектору с абсциссой 2 будет иметь абсциссу -2 (-2). Нулевой вектор будет иметь абсциссу 0.

Способы вычисления абсциссы

Если вектор задан своими координатами, то абсцисса равна значению первой координаты.
Если вектор задан начальной точкой A(x₁, y₁) и конечной точкой B(x₂, y₂), то абсцисса вектора AB вычисляется по формуле x₂ - x₁.
Если вектор задан его направляющими косинусами α, β, γ и длиной вектора |AB|, где A - начальная точка, B - конечная точка, то абсцисса вектора AB вычисляется по формуле x = |AB| * α.
Если вектор задан в проекциях на оси OX и OY, то абсцисса вектора равна его проекции на ось OX.

Таким образом, абсцисса вектора может быть вычислена различными способами, в зависимости от способа задания вектора и доступных данных.

Соотношение абсциссы и координатной оси

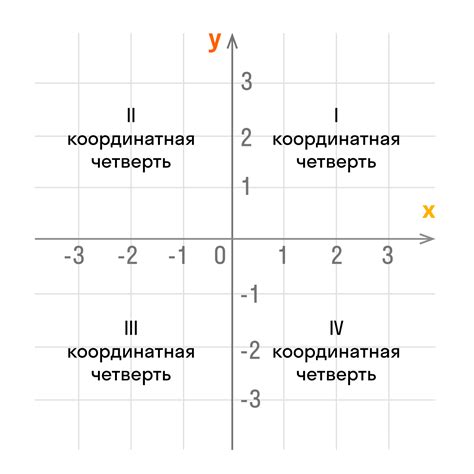
При задании абсциссы числовое значение размещается вдоль координатной оси OX. Если вектор направлен вправо, то его абсцисса будет положительной; если влево, то отрицательной. Если вектор параллелен OX, то его абсцисса будет равна нулю.

Соотношение между абсциссой и координатной осью может быть представлено следующим образом:

Положительное значение абсциссы означает, что точка, задаваемая вектором, находится справа от начала координатной оси OX.
Отрицательное значение абсциссы означает, что точка, задаваемая вектором, находится слева от начала координатной оси OX.
Нулевое значение абсциссы указывает на то, что точка, задаваемая вектором, находится на самой координатной оси OX.

Например, если вектор v имеет абсциссу x = 4, это означает, что конец вектора находится на расстоянии 4 единицы вправо от начала координатной оси OX.

Значение абсциссы вектора

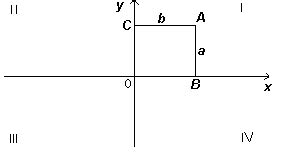
Значение абсциссы вектора показывает, насколько удален конец вектора по горизонтали от начала координат. Если начало вектора находится в точке (x1, y1), а конец – в точке (x2, y2), то значение абсциссы равно разности x-координат этих точек: x = x2 - x1.

Значение абсциссы вектора может быть положительным, отрицательным или нулевым, в зависимости от направления движения конца вектора относительно начала координат. Если конец вектора значительно смещен направо от начала координат, значение абсциссы будет положительным. В случае, если конец вектора находится левее начала координат, значение абсциссы будет отрицательным. Если начало и конец вектора находятся на одной вертикальной прямой, значение абсциссы будет равно нулю.

Значение абсциссы вектора позволяет определить его положение на координатной плоскости и использовать в дальнейших расчетах и анализе геометрических задач и физических процессов.

Абсцисса вектора в пространстве

Абсцисса может быть положительной, отрицательной или нулевой величиной, в зависимости от положения вектора относительно начала координат. Положительное значение абсциссы соответствует вектору, направленному вправо от начала координат, отрицательное значение - влево, а нулевое значение - самому началу координат.

Абсцисса вектора имеет несколько основных свойств:

Абсолютное значение: абсцисса вектора представляет собой числовую величину, которая может быть выражена безразмерным числом.
Относительное значение: абсцисса вектора зависит от выбранной системы координат, поэтому ее значение может изменяться при переходе от одной системы координат к другой.
Взаимное распределение: значения абсцисс у разных векторов могут быть как одинаковыми, так и различными в зависимости от положения векторов на числовой оси.

Примеры использования абсциссы вектора:

Пример 1:

Пусть у нас есть вектор AB в трехмерном пространстве, начало которого находится в точке с координатами (2, 4, -1), а конец - в точке с координатами (5, 2, 3). Чтобы найти абсциссу этого вектора, мы должны рассмотреть только первую координату начала и конца вектора. Тогда абсцисса вектора AB будет равна 5-2=3.

Пример 2:

Пусть у нас есть два вектора CD и EF в плоскости, начало которых находится в точке с координатами (1, 2) и (4, 5) соответственно, а конец - в точке с координатами (5, 6) и (9, 10) соответственно. Абсциссы этих векторов можно найти, рассмотрев только первую координату начала и конца векторов. Тогда абсцисса вектора CD будет равна 5-1=4, а абсцисса вектора EF - 9-4=5.