Биквадратное уравнение - это уравнение, которое содержит вторую степень переменной, её вторую степень и свободный член. В математике оно может быть представлено следующей формулой: ax4 + bx2 + c = 0, где a, b и c - коэффициенты, а x - переменная.
Решение биквадратного уравнения включает в себя два шага. В первом шаге необходимо заменить переменную, чтобы уравнение привелось к квадратному виду. Для этого вводят новую переменную, скажем y, такую что y = x2. Подставляя выражение для y вместо x2 в исходное уравнение, получаем квадратное уравнение относительно y: ay2 + by + c = 0.
Во втором шаге необходимо решить полученное квадратное уравнение относительно y. Это можно сделать с помощью формулы дискриминанта или методом завершения квадратного трехчлена. После нахождения значения y, можно найти значение x, восстановив его через замену x = √y.
Биквадратные уравнения могут возникать при моделировании некоторых физических процессов или решении конкретных задач. Они являются важным инструментом в математике и имеют широкое применение в различных областях науки.
Биквадратное уравнение: основные понятия
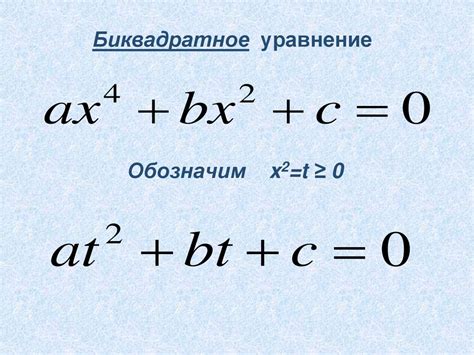
ax4 + bx2 + c = 0,
где a, b и c - коэффициенты уравнения, причем коэффициент a не равен нулю.
Решение биквадратного уравнения может быть получено с помощью замены переменной. Назовем переменную x2 равной y. После такой замены исходное уравнение примет вид:
ay2 + by + c = 0.
Теперь можно решить полученное квадратное уравнение относительно y с помощью дискриминанта и извлечения квадратного корня. Затем найденные значения y подставляются обратно в исходную замену x2 = y, тем самым получая значения переменной x.
Необходимо учитывать, что биквадратное уравнение может иметь нулевой дискриминант, что означает отсутствие реальных корней. Также возможны случаи, когда решение уравнения может быть найдено только при учете комплексных чисел, если дискриминант отрицательный.
Также важно отметить, что биквадратное уравнение может иметь несколько решений или же не иметь решений в зависимости от значений коэффициентов a, b и c.
Как выглядит биквадратное уравнение

ax4 + bx2 + c = 0
Здесь a, b и c - это коэффициенты уравнения, которые могут быть любыми действительными числами. При этом, чтобы уравнение было биквадратным, коэффициент a не должен быть равен нулю.
Биквадратное уравнение содержит два члена, возводящихся в квадрат, а именно биномы x4 и x2. Эти члены могут быть связаны с переменной x различными коэффициентами.
Решение биквадратного уравнения может быть достигнуто путем замены переменной x2 = y. Это приводит уравнение к квадратному виду:
ay2 + by + c = 0
Решение этого квадратного уравнения может быть получено с использованием обычных методов решения квадратных уравнений, таких как формула корней или законченный квадрат.
Примеры биквадратных уравнений:

1) Уравнение вида ax4 + bx2 + c = 0
- Пример 1: x4 - 7x2 + 10 = 0
- Пример 2: 2x4 + 5x2 - 3 = 0
2) Уравнение вида ax4 + bx2 = 0
- Пример 1: 3x4 - 9x2 = 0
- Пример 2: x4 + 4x2 = 0
3) Уравнение вида ax4 + c = 0
- Пример 1: 2x4 + 7 = 0
- Пример 2: x4 - 13 = 0
Как решить биквадратное уравнение в общем виде

Биквадратное уравнение имеет вид:
ax4 + bx2 + c = 0
Для решения биквадратного уравнения в общем виде можно использовать замену переменной. Пусть:
y = x2
После этой замены исходное уравнение примет вид:
ay2 + by + c = 0
Таким образом, мы свели биквадратное уравнение к квадратному уравнению.
Для решения квадратного уравнения вида ay2 + by + c = 0 можно воспользоваться формулой дискриминанта:
y = (-b ± √(b2 - 4ac)) / 2a
Полученные значения y будут корнями квадратного уравнения, а значит, и корнями исходного биквадратного уравнения.
Далее, для каждого найденного значения y нужно найти соответствующие значения x с помощью замены переменной:
x = ±√y
Итак, решение биквадратного уравнения в общем виде состоит из двух шагов:
- Находим значения y как корни квадратного уравнения ay2 + by + c = 0 с помощью формулы дискриминанта.
- Для каждого значения y находим соответствующие значения x с помощью формулы x = ±√y.
Таким образом, мы получаем все корни биквадратного уравнения в общем виде.
Методы решения биквадратного уравнения

Для решения биквадратного уравнения существуют несколько методов, в зависимости от его формы и коэффициентов.
- Метод подстановки: Этот метод заключается в замене неизвестной переменной на новую переменную, чтобы свести биквадратное уравнение к квадратному. Затем решается полученное квадратное уравнение и находятся корни исходного биквадратного уравнения.
- Метод домножения: При использовании этого метода биквадратное уравнение приводится к уравнению вида (ax^2 + bx + c)^2 = d, где a, b, c и d - известные коэффициенты. После раскрытия скобок получается квадратное уравнение, которое можно решить с использованием известных методов решения квадратных уравнений.
- Метод замены переменных: В этом методе проводится замена переменной, чтобы упростить биквадратное уравнение. Затем решается полученное упрощенное уравнение и найденные значения переменной подставляются обратно для нахождения корней исходного уравнения.
Выбор метода решения биквадратного уравнения зависит от его формы и коэффициентов. Иногда один метод может быть проще и эффективнее, чем другой. Важно учитывать особенности каждого метода и применять их в зависимости от поставленной задачи.
Решение биквадратного уравнения при помощи формул

Для решения биквадратного уравнения вида ax^4 + bx^2 + c = 0, можно использовать специальную формулу, которая позволяет найти значения переменной x.
Формула для решения биквадратного уравнения имеет вид:
x2 = (-b ± √(b2 - 4ac)) / 2a
где a, b и c - коэффициенты уравнения.
Для начала необходимо вычислить дискриминант ∆ = b2 - 4ac. Если значение дискриминанта меньше нуля, то биквадратное уравнение не имеет решений в множестве действительных чисел.
Если дискриминант равен нулю, то формула для решения принимает еще одну форму:
x = -b/2a
В этом случае уравнение имеет одно решение.
Если же дискриминант больше нуля, то формула дает два различных решения: одно с положительным значением и одно с отрицательным.
Подставляя найденные значения x в исходное уравнение, можно проверить корректность решения.
Практическое применение биквадратных уравнений
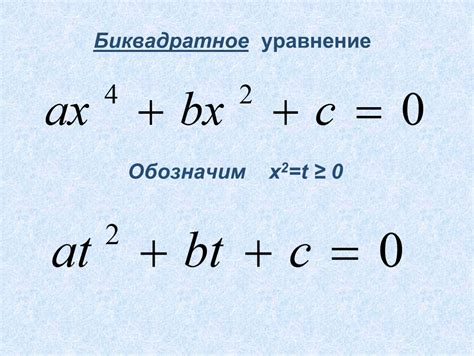
Одно из практических применений биквадратных уравнений заключается в моделировании движения объектов. Например, при изучении траектории снаряда в физике или при анализе движения частицы в математической модели.
Биквадратные уравнения также находят свое применение в теории вероятностей и статистике. Вероятность событий в некоторых случаях может быть описана с использованием биквадратных уравнений.
В инженерных расчетах и в науке о материалах биквадратные уравнения используются для решения задач, связанных с определением характеристик материалов и реакций структур на воздействие нагрузок.
Кроме того, биквадратные уравнения находят применение в оптике, аэродинамике и других отраслях науки и техники.
Все эти примеры подчеркивают важность понимания и умения решать биквадратные уравнения в различных областях науки и практического применения математики.
Особенности решения биквадратного уравнения
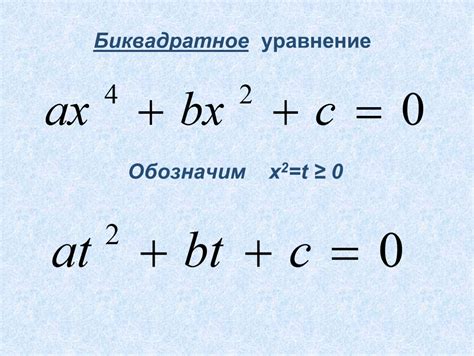
ax4 + bx2 + c = 0
Решение биквадратного уравнения может быть получено с использованием метода замены переменных и факторизации. Этот процесс может усложниться из-за нечетности коэффициентов a, b и c, поэтому следует учитывать некоторые особенности при решении биквадратного уравнения.
Одна из особенностей решения биквадратного уравнения заключается в необходимости выполнения дополнительных шагов в процессе факторизации. После замены переменной и приведения уравнения к квадратному виду, необходимо провести дополнительную факторизацию получившегося выражения.
Еще одна особенность решения биквадратного уравнения связана с возможностью появления отрицательных корней. При решении уравнения могут получиться комплексные числа, если дискриминант квадратного уравнения отрицательный. В таком случае биквадратное уравнение не имеет решений в вещественных числах.
Итак, решение биквадратного уравнения требует проведения дополнительных действий при факторизации и возможно появления комплексных корней при отрицательном дискриминанте. Учитывая эти особенности, можно успешно решить биквадратное уравнение и найти его корни.
Полезные советы для решения биквадратных уравнений

Биквадратные уравнения могут быть сложными и запутанными, но с правильным подходом и некоторыми полезными советами их можно решить. Вот некоторые полезные советы для решения биквадратных уравнений:
1. Внимательно прочитайте уравнение и убедитесь, что оно находится в стандартной форме. Биквадратное уравнение имеет вид ax^4 + bx^2 + c = 0, где a, b и c - коэффициенты, которые могут быть положительными, отрицательными или нулевыми числами.
2. Попробуйте провести замену переменной, чтобы упростить уравнение. Некоторые замены, которые могут быть полезны, включают замену x^2 = t или x^2 = u^2.
3. Используйте методы факторизации для разложения биквадратного уравнения на более простые множители. Если это возможно, выражение может быть разложено в виде (mx^2 + nx + p)(qx^2 + rx + s) = 0, где m, n, p, q, r и s - коэффициенты.
4. Примените методы решения квадратных уравнений к полученным множителям. Решение полученных квадратных уравнений может дать значения переменной x.
5. Убедитесь, что все решения уравнения являются допустимыми. Иногда в процессе решения биквадратного уравнения могут возникать такие значения переменной x, которые не удовлетворяют исходному уравнению. Проверьте найденные значения, подставив их в исходное уравнение и убедившись, что оно выполняется.
Используя эти полезные советы, вы сможете справиться с решением биквадратных уравнений. Практика и упорство помогут вам стать лучшим в решении таких уравнений и находить их решения более быстро и эффективно.




