Черточка над множествами - это символ, который обозначает операцию разности между двумя множествами. Обычно это горизонтальная линия, которая ставится между множествами и указывает на то, что элементы, принадлежащие одному множеству, не принадлежат другому. Черточка над множествами используется в математике и логике для обозначения разности между двумя множествами.
Например, если у нас есть два множества A и B, где А = {1, 2, 3, 4} и В = {3, 4, 5}, то операцию разности можно записать следующим образом: A \ B. Результатом этой операции будет множество, включающее все элементы из A, которых нет в B. В данном случае разность между A и B будет равна {1, 2}.
Важно понимать, что черточка над множествами указывает только на отсутствие элементов одного множества в другом. Она не учитывает порядок элементов и повторяющиеся значения.
Использование черточки над множествами может быть полезным в ряде задач. Например, она может быть использована для нахождения пересечения или объединения двух множеств. Она также позволяет вычислять разность между множествами и определять отношения включения и невключения между ними.
Таким образом, черточка над множествами представляет собой важный инструмент в математике и логике, который позволяет устанавливать отношения между двумя множествами и вычислять операции с ними.
Черточка над множествами: зачем она нужна
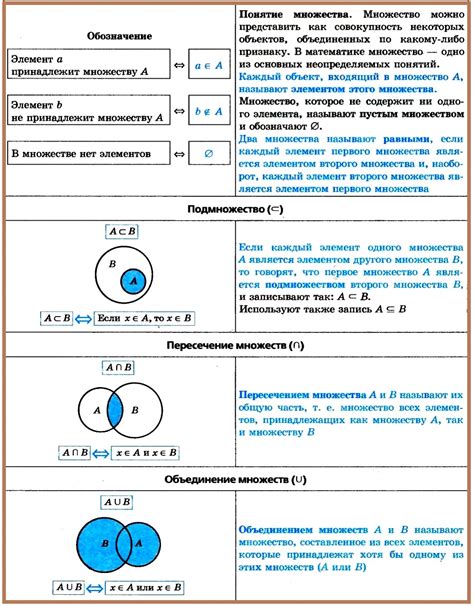
Одним из основных применений черточки над множествами является обозначение операции дополнения множества. Когда над множеством A ставится черточка, обозначается комплементарное множество, то есть множество всех элементов, которые не принадлежат множеству A. Такое множество обычно обозначается как A с чертой сверху.
Также, черточка над множествами может использоваться для обозначения операции пересечения множеств. Если множество A пересекается с множеством B, то результатом операции будет множество, состоящее из элементов, принадлежащих и A, и B. При записи этой операции над множествами, над пересекаемыми множествами ставится черточка.
Черточка над множествами также используется для обозначения операции разности множеств. При разности множеств, из одного множества вычитается другое множество, и результатом будет новое множество, состоящее из элементов, принадлежащих первому множеству, но не принадлежащих второму. При записи этой операции, над вычитающим и вычитаемым множествами также ставится черточка.
Использование черточки над множествами облегчает запись и чтение математических формул, делая их более ясными и понятными. Она позволяет уточнять операции и свойства множеств, и обозначать их более компактным и удобным способом.
Для обозначения отношений между множествами
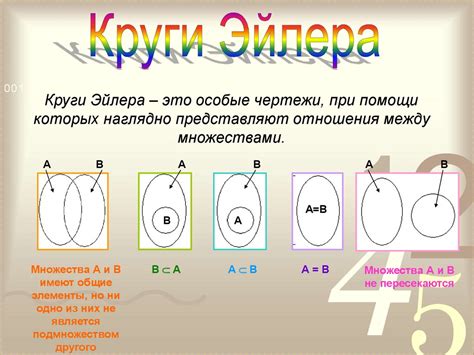
Черточка над множеством используется для обозначения отношений между множествами. Она часто используется в математике и логике для указания различных связей между наборами элементов.
Некоторые общие отношения, которые могут быть обозначены с помощью черточки над множеством:
- Подмножество - если множество A является подмножеством множества B, то это обозначается как A ⊆ B. Это означает, что каждый элемент множества A также принадлежит множеству B.
- Собственное подмножество - если множество A является собственным подмножеством множества B, то это обозначается как A ⊂ B. В этом случае A является подмножеством B, но также имеет хотя бы один элемент, который не принадлежит множеству B.
- Пересечение - если множество A и множество B имеют хотя бы один общий элемент, то их пересечение обозначается как A ∩ B.
- Объединение - объединение множеств А и В обозначается как A ∪ B и включает в себя все элементы обоих множеств.
- Отрицание - обозначение отрицания множества А в виде ¬А указывает на все элементы, которые не принадлежат множеству А.
- Дополнение - дополнение множества А обозначается как A'. Включает в себя все элементы, которые не принадлежат множеству А относительно универсального множества.
Черточка над множествами - это удобный и понятный способ обозначения отношений между множествами в математике и логике.
Для обозначения операций над множествами
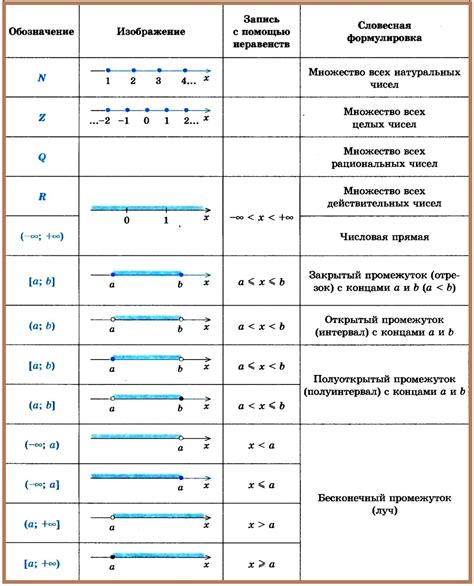
Черточка над множествами используется для обозначения операций над множествами. Она указывает на то, что представленное под ней множество подвергается определенной операции или принадлежит определенному классу множеств.
Основные операции над множествами, обозначаемые черточкой, включают:
- Объединение множеств - обозначается символом ∪. Например, A ∪ B обозначает объединение множеств A и B.
- Пересечение множеств - обозначается символом ∩. Например, A ∩ B обозначает пересечение множеств A и B.
- Разность множеств - обозначается символом \. Например, A \ B обозначает разность множеств A и B, то есть все элементы, принадлежащие множеству A, но не принадлежащие множеству B.
- Дополнение множества - обозначается символом '. Например, A' обозначает дополнение множества A, то есть все элементы, не принадлежащие множеству A.
Примеры использования черточки над множествами:
- A ∪ B = {1, 2, 3, 4}
- A ∩ B = {2, 3}
- A \ B = {1}
- B' = {5, 6, 7}
Таким образом, черточка над множествами играет важную роль в математике и позволяет удобно обозначать операции над множествами и их свойства.




