При решении уравнений и задач по математике мы иногда сталкиваемся с выражениями, в которых перед корнем стоит цифра. Например, √5 или √7. Что же означает эта цифра?
Цифра, стоящая перед корнем, называется степенью корня. Степень корня показывает, какую операцию следует выполнить над корнем, чтобы вычислить значение всего выражения.
Например, если перед корнем стоит цифра 2 (√2), это означает, что нужно выполнить операцию извлечения квадратного корня. Извлечение квадратного корня из числа 2 можно записать как √2 = √(2*2) = 2.
Таким образом, степень корня указывает на то, какую степень нужно взять из числа, чтобы получить значение корня.
Иногда вместо числа перед корнем может использоваться буква. В этом случае буква обозначает переменную, а степень корня указывает на степень переменной. Например, √x^2 означает извлечение квадратного корня из квадрата переменной x.
Теперь мы знаем, что означает цифра перед корнем в выражении и как ее использовать для вычисления значения этого выражения.
Значение цифры перед корнем в выражении

Цифра, расположенная перед корнем в выражении, обычно обозначает степень корня. Корень выражения представляет собой операцию, обратную возведению в степень. Например, если у нас есть выражение √9, то корнем этого выражения будет число 3, так как 3 в квадрате равно 9.
В общем случае, число перед корнем задает степень корня. Например, для выражения √64, число 2 указывает на то, что мы берем квадратный корень из числа 64. То есть, 2 второй степени равно 4, а 4 второй степени равно 64.
Если перед корнем стоит цифра отличная от 2, то это указывает на то, что мы берем корень соответствующей степени. Например, для выражения ∛27, число 3 указывает на то, что мы берем кубический корень из числа 27. То есть, 3 третьей степени равно 27, а -3 третьей степени равно -27.
Таким образом, значение цифры перед корнем в выражении имеет важное значение при определении результата вычислений. Необходимо учитывать степень корня при решении математических выражений, содержащих корни.
Определение числа перед корнем

Число, стоящее перед корнем в выражении, называется коэффициентом или множителем. Оно указывает, во сколько раз нужно умножить значение корня.
Например, в выражении √9 коэффициент равен 1, так как √9 = 3. А в выражении 2√9 коэффициент равен 2, поэтому 2√9 = 6.
Коэффициент добавляется перед корнем, чтобы увеличить или уменьшить его значение. Он может быть как положительным, так и отрицательным числом.
Часто коэффициент перед корнем используется для упрощения исходного выражения. Например, вместо √18 можно записать 3√2. Здесь коэффициент равен 3, а корень √2 остается без изменений. Это позволяет сократить количество символов в выражении.
Также стоит отметить, что если в выражении нет числа перед корнем, то коэффициент считается равным 1. Например, √16 равносильно 1√16, что равно 4.
Понятие корня в математике
В математике корень выражения представляет собой значение, при подстановке которого равенство уравнения выполняется. Цифра, находящаяся перед корнем, указывает степень, в которую нужно возвести найденное значение для получения исходного выражения.
Корень может быть выражен как положительное, так и отрицательное число. Обычно, если ничего не указано, под корнем понимается положительное значение.
Примером может служить выражение √9. Здесь цифра 9 является основанием, а корень равен 2. Так как перед корнем отсутствует цифра, это означает что степень, в которую нужно возвести корень, равна 2.
Понимание понятия корня позволяет решать различные уравнения, а также использовать его в различных областях науки и техники.
| Корень | Основание | Степень |
|---|---|---|
| √4 | 4 | 2 |
| √25 | 25 | 2 |
| √81 | 81 | 2 |
Виды корней
Корень математического выражения выражает число, которое при возведении в некоторую степень даёт исходное число. Однако, не все корни одинаковы и несут одно и то же значение. Цифра перед корнем придаёт выражению особый смысл и определяет его вид.
Квадратный корень
Если перед корнем стоит цифра 2, то это значит, что выражение является квадратным корнем. Квадратный корень из числа а обозначается как √a.
Например, √9 равен 3, потому что 3 * 3 = 9.
Кубический корень
Если перед корнем стоит цифра 3, то это значит, что выражение является кубическим корнем. Кубический корень из числа а обозначается как ³√a.
Например, ³√27 равен 3, потому что 3 * 3 * 3 = 27.
Неквадратные корни
Если перед корнем стоит любая другая цифра (кроме 2 и 3), то это значит, что выражение является корнем n-ой степени. Корень n-ой степени из числа а обозначается как n√a.
Например, 4√16 равен 2, потому что 2 * 2 * 2 * 2 = 16.
Обратите внимание, что когда перед корнем не указана цифра, как, например, √25, это означает, что речь идет о квадратном корне, то есть этот корень подразумевает цифру 2.
Корень в степенной функции
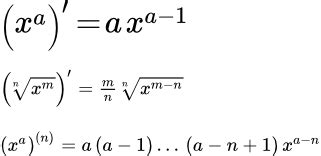
Цифра перед корнем в выражении указывает на степень, в которую нужно возвести корень. Например, если перед корнем стоит число 2, то это означает, что нужно извлечь квадратный корень из числа или выразить его в степени 1/2.
Корень - это математическая операция, обратная возведению в степень. Из числа в степени получается исходное число. Например, 2^2 = 4, а √4 = 2.
Чтобы выполнить корень в степенной функции, следует использовать правила алгебры: извлекать корень можно только из положительных чисел, если степень является нечетной, то результат корня будет иметь тот же знак, что и исходное число, если степень является четной, то результат корня всегда положительный.
При использовании корней степени можно использовать различные обозначения: в общем случае корень степени n из числа a обозначается как √na или с помощью знака корня и индекса: n√a.
Решение уравнений с корнем

В некоторых уравнениях можно встретить корень, который представлен в виде дроби, степени или даже под корнем.
Если перед корнем стоит цифра, это означает, что нужно извлечь корень из числа, которое находится под корнем. Для решения таких уравнений необходимо выполнить следующие шаги:
- Выделить число, которое находится под корнем.
- Извлечь корень из этого числа, используя соответствующую степень корня.
- Учесть знак перед корнем.
- Решить оставшуюся часть уравнения.
Пример:
Уравнение 5√x = 15
- Выделение числа под корнем: √x = 15/5 = 3.
- Извлечение корня: x = 3^2 = 9.
- Учет знака: в данном случае нет знака перед корнем, поэтому знак остается положительным.
- Решение оставшейся части уравнения: в данном случае нет оставшейся части уравнения.
Таким образом, решением уравнения 5√x = 15 является x = 9.
Интерпретация результатов с корнем

Окончательный результат выражения с корнем может быть интерпретирован по-разному в зависимости от наличия цифры перед корнем.
Если перед корнем стоит отрицательное число, то результат будет комплексным числом. Комплексные числа имеют мнимую и действительную части, и представляются в виде a + bi, где a и b - вещественные числа, а i - мнимая единица, обозначающая квадратный корень из -1.
Если перед корнем стоит положительное число, то результат будет вещественным числом. Вещественные числа представляют собой числа с плавающей точкой, которые могут быть положительными или отрицательными, исключая мнимую часть.
В случае, если перед корнем стоит 0, то результатом будет само число 0.
Примеры использования корня в выражениях

| Выражение | Значение |
|---|---|
| √9 | 3 |
| 2√25 | 10 |
| 3√27 | 3 |
| 4√256 | 4 |
В этих примерах, число перед корнем указывает на степень корня. Например, в выражении 2√25, число 2 указывает на квадратный корень, 25 - значение, подлежащее извлечению корня. Результатом выполнения данного выражения будет число 10, так как квадратный корень из 25 равен 5, а значение выражения равно 2 * 5 = 10.
Аналогично, в выражении 3√27, число 3 указывает на кубический корень, а результатом выполнения этого выражения будет число 3, так как кубический корень из 27 равен 3.
Таким образом, число перед корнем в выражении используется для указания степени корня и определяет, сколько раз надо извлечь корень из исходного числа.




