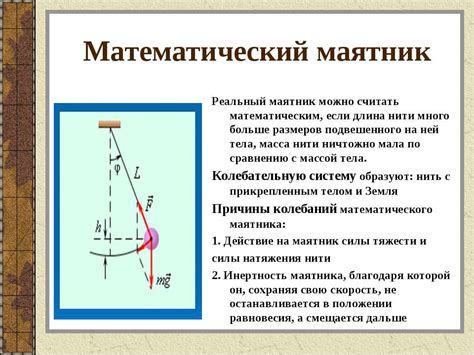
Математический маятник - это физическая система, используемая в механике для исследования колебаний. Он представляет собой точечную массу, подвешенную на тонкой нерастяжимой нити или стержне. Математический маятник является одним из фундаментальных источников понимания основных законов колебаний и явлений.
Принцип работы математического маятника основан на простых физических законах. Под действием гравитационной силы маятник начинает колебаться из стороны в сторону. Его колебания описываются уравнением гармонического осциллятора, которое зависит от длины нити, ускорения свободного падения и начального отклонения маятника от равновесия.
«Математический маятник показывает, как изменяется положение системы в зависимости от различных факторов, таких как длина нити, масса маятника и амплитуда колебаний. Это позволяет исследователям проводить численные расчеты и разрабатывать теоретические модели для объяснения различных физических явлений».
Математические маятники находят широкое применение в научных исследованиях, инженерии и повседневной жизни. Они используются для изучения законов колебаний и визуализации математических моделей. Математические маятники также применяются в физических лабораториях для обучения студентов и демонстрации принципов работы колебательных систем.
Математический маятник: что это такое
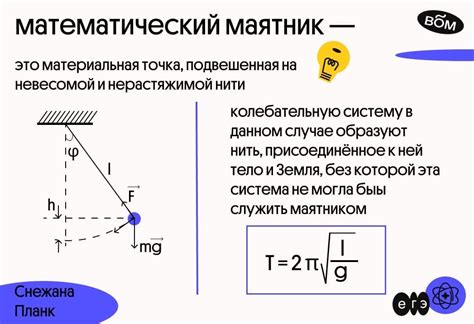
Математический маятник является одним из наиболее простых и изученных объектов в физике, и его движение тщательно описывается уравнением математического маятника – уравнением гармонического осциллятора. Оно позволяет рассчитать период и частоту колебаний маятника, а также его амплитуду.
Идеализированный математический маятник не учитывает трение, сопротивление воздуха и другие внешние факторы, поэтому он используется в основном для теоретических расчетов и моделирования.
Применение математического маятника находит в широком спектре областей, включая физику, инженерию, астрономию и механику. Он помогает в понимании многих физических законов и явлений, таких как резонанс, демпфирование и динамическая устойчивость. Кроме того, математический маятник используется для создания точных часов и измерения ускорения свободного падения.
| Применение математического маятника: |
|---|
| Физика |
| Инженерия |
| Астрономия |
| Механика |
Принцип работы математического маятника

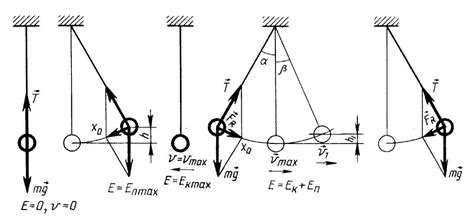
Принцип работы математического маятника основан на законе сохранения энергии. При начальном отклонении маятника от положения равновесия, его потенциальная энергия превращается в кинетическую энергию. Когда маятник достигает самой нижней точки своего движения, его кинетическая энергия максимальна, а потенциальная энергия минимальна. В этот момент маятник начинает движение назад, и процесс повторяется, пока вся энергия не будет потеряна из-за трения и сопротивления воздуха.
Математический маятник может быть описан при помощи математического уравнения, называемого уравнением гармонического осциллятора. Оно позволяет определить период колебаний маятника и его зависимость от длины нити, силы тяжести и начального отклонения.
Математические маятники широко применяются в научных исследованиях, включая физику, инженерию и астрономию. Они используются для измерения времени, проверки математических моделей и проведения физических экспериментов. Также математические маятники являются частью некоторых музейных экспозиций и аттракционов.
Интересные факты о математическом маятнике
1. Великие ученые использовали математический маятник для исследований.
Математический маятник был не только предметом изучения, но и прекрасным инструментом для проведения различных экспериментов. Некоторые великие ученые, такие как Исаак Ньютон и Галилео Галилей, использовали математический маятник для изучения законов движения и гравитации. Благодаря этому наблюдению, они смогли сформулировать важные теории и законы, которые до сих пор используются в науке.
2. Математический маятник может быть использован для измерения времени.
Изначально математический маятник был разработан для измерения времени. Он может служить в качестве точного метронома или часов, основанных на качке маятника. Эта характеристика позволяет использовать математический маятник для создания механизмов, которые показывают точное время или используются для синхронизации других механизмов, таких как показания часов или метронома.
3. Математический маятник является приближением к идеальной системе.
Математический маятник является абстракцией, которая описывает идеализированную систему, в которой силы сопротивления воздуха и трения отсутствуют. Математический маятник предоставляет ученым простую модель для исследования основных принципов и законов механики. Он позволяет изучать закономерности движения без сложных факторов, которые влияют на реальные системы.
4. Математический маятник используется в физических и математических исследованиях.
Математический маятник находит применение в различных научных областях, таких как физика и математика. Он помогает исследователям изучать различные аспекты движения и энергии. Физики используют математический маятник для изучения законов гравитации, свободного падения и колебаний. Математики используют его для иллюстрации математических принципов и формул.
5. Математический маятник используется в конструировании различных устройств.
Математический маятник является базовым элементом в конструировании различных устройств и механизмов. Он используется в часах, механических игрушках, метрономах, маятниках для контроля вибрации и многом другом. Благодаря своей стабильности и предсказуемости, математический маятник является незаменимым элементом в создании механических устройств.
6. Математический маятник может быть используется для измерения ускорения свободного падения.
Исследователи используют математический маятник для измерения ускорения свободного падения, которое является константой и составляет около 9,8 м/с² на поверхности Земли. Он позволяет с высокой точностью определить это значение и использовать его для решения различных физических задач.
7. Математический маятник может иметь различные длины и массы.
Математический маятник может быть разной длины и массы. Изменение этих параметров может повлиять на его период колебаний и амплитуду движения. Исследование зависимости этих параметров позволяет понять основные законы и принципы, которые описывают движение.
История развития математического маятника
В 1583 году Галилео Галилей, итальянский ученый и философ, обратил внимание на период колебания светильника в Пизанском кафедральном соборе. Он заметил, что период колебания светильника зависит только от длины подвеса и не зависит от массы или амплитуды колебаний. Это наблюдение привело Галилея к формулированию закона, который стал известен как закон гармонического движения математического маятника.
За последующие века математический маятник стал неотъемлемой частью физического образования и исследований. Он использовался для иллюстрации и демонстрации различных принципов физики и математики, таких как законы сохранения энергии и механики.
В настоящее время математический маятник находит широкое применение в образовательных учреждениях, научных исследовательских институтах и лабораториях, а также в различных устройствах и приборах. Он используется для изучения законов колебательного движения, определения силы тяжести и различных математических моделей.
| Дата | Событие |
|---|---|
| 1583 г. | Галилео Галилей открыл закон гармонического движения математического маятника. |
Уравнение математического маятника

Математический маятник можно описать с помощью уравнения, которое позволяет вычислить его движение в зависимости от начальных условий.
Уравнение математического маятника выглядит следующим образом:
- Для малых углов отклонения:
момент инерции × угловое ускорение = момент силы тяжести × плечо силы
- Для больших углов отклонения:
момент инерции × угловое ускорение + коэффициент сопротивления × скорость = момент силы тяжести × плечо силы
Здесь момент инерции определяется массой маятника и его геометрическими характеристиками, угловое ускорение - изменение угловой скорости со временем, момент силы тяжести - произведение массы маятника на ускорение свободного падения, а плечо силы - расстояние от точки подвеса до центра масс маятника.
Уравнение математического маятника позволяет предсказать его движение и поведение в различных условиях. Оно широко применяется в науке и технике, в том числе в физике, механике и робототехнике.




