В процессе решения различных математических задач часто возникает необходимость разделить некоторое количество объектов на равные части. Это может быть полезно, например, при распределении ресурсов, разбиении данных для их последующей обработки или при вычислении статистических параметров.
Для разделения объектов на равные части существуют различные методы, и выбор определенного подхода зависит от поставленной задачи. Один из самых простых и понятных методов - это деление на равные группы. В этом случае объекты разбиваются на некоторое количество групп, так что каждая группа содержит одинаковое количество элементов.
Другим способом разделения на равные части является деление на равные интервалы. В этом случае объекты разбиваются на интервалы определенного размера, при этом каждый интервал содержит одинаковое количество элементов. Этот метод часто применяется при построении гистограмм или при анализе распределения данных.
Важно отметить, что при использовании любого из этих методов нужно учитывать особенности задачи и конкретные требования, так как они могут влиять на точность и эффективность итогового решения.
Методы разделения на равные части
Для разделения объекта на равные части существует несколько методов, которые могут быть использованы в разных ситуациях:
- Метод деления на равные части по количеству
- Метод деления на равные части по длине
- Метод деления на равные части по площади
- Метод деления на равные части по объему
При использовании метода деления на равные части по количеству объект разделяется на указанное количество равных частей. Примером может быть разделение шоколадной плитки на несколько кусков, каждый из которых имеет одинаковый вес.
Метод деления на равные части по длине подразумевает разделение объекта на равные по длине части. Например, при делении веревки на несколько частей, каждая из них будет иметь одинаковую длину.
Метод деления на равные части по площади предполагает разделение объекта на равные по площади части. Например, при разделении прямоугольника на несколько равных по площади квадратов.
Метод деления на равные части по объему применяется в случаях, когда требуется разделить объект на равные по объему части. Примером может быть разделение куба на несколько равных по объему параллелепипедов.
Выбор метода разделения на равные части зависит от конкретной задачи и характеристик объекта, который необходимо разделить.
Метод деления на равные отрезки
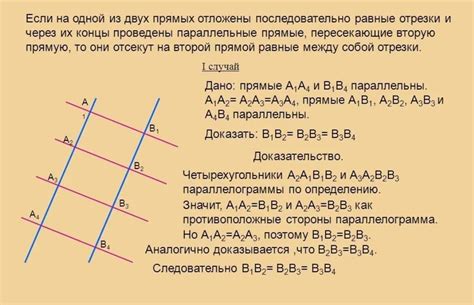
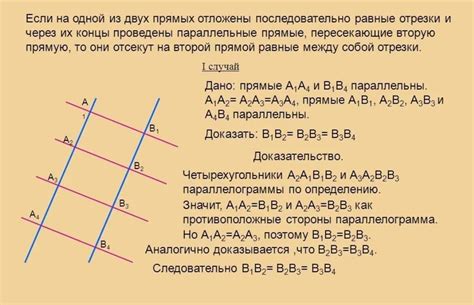
Для применения этого метода нужно знать начальную точку отрезка, конечную точку и количество желаемых равных отрезков.
1. Найдите длину заданного отрезка, которую можно вычислить как разность координат начальной и конечной точек.
2. Разделите длину отрезка на количество желаемых равных отрезков, чтобы определить длину каждого отрезка.
3. Расчитайте координаты начальной точки первого равного отрезка как координаты начальной точки заданного отрезка.
4. Прибавьте длину каждого отрезка к координатам начальной точки, чтобы определить координаты конечной точки каждого отрезка.
5. Повторите шаги 3 и 4 для оставшихся равных отрезков, изменяя начальные и конечные точки соответственно.
Метод деления на равные отрезки широко применяется в различных областях, включая геометрию, математику, физику и программирование.
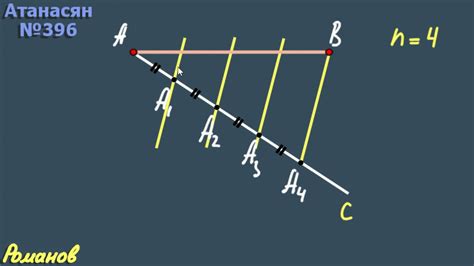
Пример: Пусть задан отрезок AB с координатами (1, 2) и (7, 2). Необходимо разделить этот отрезок на 4 равных части.
1. Длина отрезка AB: 7 - 1 = 6.
2. Длина каждого равного отрезка: 6 / 4 = 1.5.
3. Начальная точка первого равного отрезка: (1, 2).
4. Конечная точка первого равного отрезка: (1 + 1.5, 2) = (2.5, 2).
5. Начальная точка второго равного отрезка: (2.5, 2).
6. Конечная точка второго равного отрезка: (2.5 + 1.5, 2) = (4, 2).
7. Начальная точка третьего равного отрезка: (4, 2).
8. Конечная точка третьего равного отрезка: (4 + 1.5, 2) = (5.5, 2).
9. Начальная точка четвертого равного отрезка: (5.5, 2).
10. Конечная точка четвертого равного отрезка: (5.5 + 1.5, 2) = (7, 2).
Таким образом, исходный отрезок AB был разделен на 4 равных части с координатами (1, 2) - (2.5, 2) - (4, 2) - (5.5, 2) - (7, 2).
Метод деления на равные участки
Для совершения равномерного деления объекта или промежутка можно использовать различные подходы и алгоритмы. Наиболее распространенными методами являются:
1. Деление на равные части с помощью деления нацело.
Этот метод заключается в том, что объект или промежуток делится на равные части путем деления его длины или количества элементов на заданное количество. Например, чтобы разделить отрезок длиной 12 единиц на 4 равные части, необходимо выполнить действие 12 / 4 = 3. Полученное значение будет являться длиной каждой части.
2. Деление на равные части с помощью формулы.
Этот метод применяется в случаях, когда объект или промежуток можно представить в виде функции, уравнения или формулы. Для совершения равномерного деления используются соответствующие значения параметров, переменных или аргументов. Например, чтобы разделить график функции на 5 равных частей, нужно найти значения аргументов, при которых функция принимает одинаковые значения.
3. Деление на равные части с помощью итераций.
Этот метод заключается в последовательном делении объекта или промежутка на равные части путем повторения определенных действий, пока не будет достигнуто желаемое количество частей. Например, для разделения отрезка длиной 10 единиц на 6 равных частей можно последовательно выполнять действия: 10 / 6 = 1.666, 1.666 / 6 = 0.277, и так далее, пока не будет получено нужное количество равных частей.
Применение метода деления на равные участки позволяет равномерно распределить объект или промежуток на одинаковые части, что может быть полезно при решении различных задач и проблем.
Примеры разделения на равные части

Существует несколько методов, которые позволяют разделить объекты на равные части:
- Метод деления на количество объектов:
- Если необходимо разделить объект на определенное количество частей, можно воспользоваться данным методом. Примером может служить разделение торта на определенное количество кусочков.
- Этот метод используется, когда необходимо разделить объект на равные части по длине. Например, можно разделить веревку на 3 равные части, измерив ее длину и разделив на 3.
- В этом методе объект разделяется на равные части по площади. Например, можно разделить огород на несколько равных участков, чтобы выращивать на них разные культуры.
Это лишь некоторые примеры разделения на равные части, их можно применять в различных ситуациях в повседневной жизни и рабочей деятельности.
Разделение линии на равные отрезки
Существует несколько способов разделить линию на равные отрезки. Один из простых методов - использование таблицы. Для этого можно создать таблицу с одной строкой и несколькими столбцами. Количество столбцов определяется количеством требуемых отрезков.
| Отрезок 1 | Отрезок 2 | Отрезок 3 |
Если требуется разделить линию на большее количество равных отрезков, то количество столбцов в таблице будет соответствовать этому количеству.
При использовании этого метода важно учесть, что ширина каждого столбца должна быть равной. Для этого можно установить фиксированную ширину столбцов или использовать CSS-стили для автоматической расстановки ширины.
Другим методом разделения линии на равные отрезки является использование математической формулы. Для этого необходимо знать общую длину линии и количество требуемых отрезков. Затем длину каждого отрезка можно вычислить, разделив общую длину на количество отрезков.
Например, если общая длина линии составляет 10 единиц, и требуется разделить ее на 5 равных отрезков, то длина каждого отрезка будет равняться 2 единицам.
Такие простые методы дают возможность разделить линию на равные отрезки без использования сложных вычислений или специализированного программного обеспечения.




