При работе с графиками и анализе функций важно знать, как найти точки пересечения с осями координат. Эти точки представляют собой особую информацию о поведении функции и могут быть использованы для решения различных задач.
Точки пересечения с осями координат — это точки, в которых график функции пересекает оси координат. На графике эти точки обозначаются как (x, 0) и (0, y), где x и y — это координаты точек пересечения с осью x и осью y соответственно.
Для нахождения точек пересечения с осью x нужно решить уравнение f(x) = 0, где f(x) — это функция, заданная в уравнении. Решив уравнение, мы найдем значения x, которые соответствуют точкам пересечения с осью x.
Аналогично, для нахождения точек пересечения с осью y нужно решить уравнение f(0) = y, где f(0) — это значение функции в точке (0, y). Решив это уравнение, мы получим значения y, которые соответствуют точкам пересечения с осью y.
В статье мы рассмотрим подробные примеры и объяснения для нахождения точек пересечения с осями координат на графиках функций разных видов. Это поможет понять эту концепцию лучше и научиться применять ее в практике.
Как определить точки пересечения с осями координат
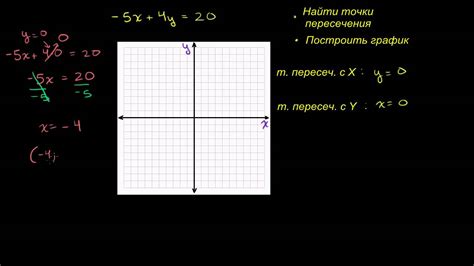
Для определения точки пересечения с осью X необходимо приравнять значение функции к нулю и решить уравнение. Результатом будет значение X, при котором функция пересекает ось X. Точка пересечения с осью X будет иметь координаты (X, 0).
Аналогично, для определения точки пересечения с осью Y необходимо приравнять значение X к нулю и решить уравнение. Результатом будет значение Y, при котором функция пересекает ось Y. Точка пересечения с осью Y будет иметь координаты (0, Y).
Например, рассмотрим функцию y = 2x - 3. Чтобы определить точки пересечения с осями координат, нужно приравнять y и x к нулю:
Для оси X: 2x - 3 = 0
2x = 3
x = 3/2
Точка пересечения с осью X: (3/2, 0)
Для оси Y: 2(0) - 3 = 0
-3 = 0
Точка пересечения с осью Y: (0, -3)
Таким образом, функция y = 2x - 3 пересекает ось X в точке (3/2, 0) и ось Y в точке (0, -3).
Определение точек пересечения с осями координат является важным инструментом в анализе функций и графиков. Это позволяет определить значения по осям и легко находить пересечения графика с осью X и осью Y.
Точки пересечения с осью X
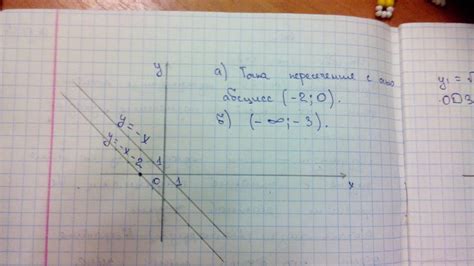
Один из способов найти точку пересечения с осью X состоит в том, чтобы решить уравнение, где Y равно нулю. Другими словами, мы ищем значения X, при которых Y равно нулю.
Если у нас есть уравнение вида Y = f(X), то точка пересечения с осью X будет являться решением следующего уравнения:
f(X) = 0.
Для решения этого уравнения мы можем использовать различные методы, включая графический, аналитический или численный. В каждом случае мы должны найти значение X, при котором функция равна нулю.
Например, рассмотрим уравнение квадратичной функции:
f(X) = X^2 - 4X + 3.
Чтобы найти точки пересечения с осью X, мы должны решить уравнение:
X^2 - 4X + 3 = 0.
Решая это уравнение аналитически или с использованием численных методов, мы найдем, что X может быть равен 1 или 3. Таким образом, точки пересечения с осью X для данной функции будут (1, 0) и (3, 0).
Точки пересечения с осью Y
Точка пересечения с осью Y представляет собой точку, в которой график функции или линии пересекает ось Y (вертикальную ось) в координатной плоскости.
Для нахождения точки пересечения с осью Y необходимо приравнять значение X к 0 и решить уравнение, полученное таким образом. Так как ось Y имеет значение X равное нулю, то положение точки пересечения будет иметь вид (0, Y), где Y - значение Y-координаты точки пересечения.
Например, рассмотрим график функции y = 2x + 3. Для нахождения точки пересечения с осью Y, приравняем Х к 0:
0 = 2x + 3
2x = -3
x = -3/2
Таким образом, точка пересечения с осью Y будет иметь координаты (0, 3).
Примеры нахождения точек пересечения с осями координат
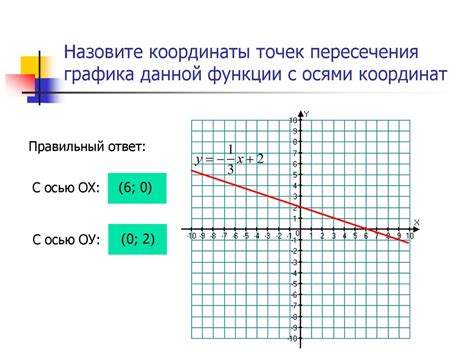
Для нахождения точки пересечения графика с осью координат, необходимо приравнять координату соответствующей оси к нулю.
Пример 1:
Рассмотрим график функции y = x^2 - 4x.
Для определения точек пересечения данной функции с осью OX, необходимо приравнять y к нулю:
x^2 - 4x = 0
Факторизуем данное уравнение:
x(x - 4) = 0
Таким образом, получаем две возможных точки пересечения графика с осью OX: x = 0 и x = 4.
Для определения точек пересечения с осью OY, необходимо приравнять x к нулю:
y = 0^2 - 4 * 0 = 0
Таким образом, получаем точку пересечения графика с осью OY: (0, 0).
Пример 2:
Рассмотрим график функции y = sin(x).
Для определения точек пересечения данной функции с осью OX, необходимо приравнять y к нулю:
sin(x) = 0
Так как синус равен нулю в точках, кратных числу π, получаем бесконечное множество точек пересечения графика с осью OX: x = kπ, где k - целое число.
Для определения точек пересечения с осью OY, необходимо приравнять x к нулю:
y = sin(0) = 0
Таким образом, получаем точку пересечения графика с осью OY: (0, 0).
Пример 3:
Рассмотрим график функции y = √(9 - x^2).
Для определения точек пересечения данной функции с осью OX, необходимо приравнять y к нулю:
√(9 - x^2) = 0
Так как корень равен нулю только при x = 9, получаем одну точку пересечения графика с осью OX: x = 9.
Для определения точек пересечения с осью OY, необходимо приравнять x к нулю:
y = √(9 - 0^2) = 3
Таким образом, получаем точку пересечения графика с осью OY: (0, 3).
Из данных примеров видно, что количество и расположение точек пересечения с осями координат зависит от графика функции и может быть различным.




