При погружении в изучение математики невозможно обойти вниманием такие понятия, как ордината и абсцисса. Эти два термина являются ключевыми в графической интерпретации функций и имеют существенное значение при анализе различных графиков.
Ордината и абсцисса - это оси координат, которые служат для определения положения точек на плоскости. Абсцисса обозначается как "x", а ордината - как "y". Они пересекаются в точке, которая называется началом координат и имеет координаты (0, 0). Направление осей указывается соответствующим знаком: вправо для положительных значений абсциссы и вверх для положительных значений ординаты.
Противоположность абсциссы и ординаты на графике может иметь разное значение в зависимости от контекста. Когда мы говорим о положительных и отрицательных значениях осей, то абсцисса и ордината противоположны друг другу. Например, отрицательные значения абсциссы будут указывать на точки, расположенные левее начала координат, а отрицательные значения ординаты - ниже нулевой отметки по оси "y".
Ордината и абсцисса имеют свойства зеркального отражения друг друга. Если, например, отразить график функции относительно оси абсцисс, то достигается зеркальное отражение графика относительно оси ординат и наоборот.
Противоположность ординаты и абсциссы в графике также может раскрываться через анализ симметрии функции. Если график функции является симметричным относительно оси абсцисс, то все точки, находящиеся по разные стороны от этой оси, будут иметь противоположные значения ординаты. Аналогично, симметричность графика относительно оси ординат указывает на противоположность абсциссы у точек, находящихся по разные стороны от этой оси.
Что означает противоположность ординаты и абсциссы на графике?
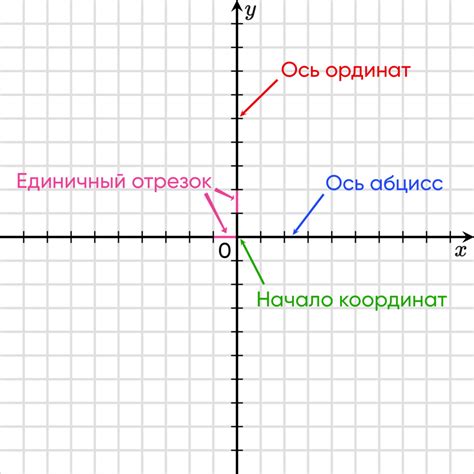
Ордината (ось y) представляет вертикальную ось и отображает значения зависимой переменной или величину, которая меняется или рассчитывается в результате других входных данных. Она располагается по вертикали и варьируется отнизу вверх.
Абсцисса (ось x) представляет горизонтальную ось и отображает значения независимой переменной или параметра, который изменяется независимо от других переменных. Она располагается по горизонтали и варьируется слева направо.
Противоположность ординаты и абсциссы на графике означает, что оси пересекаются в одной точке, которая называется началом координат. В этой точке значение ординаты равно нулю, а значение абсциссы также равно нулю. Отсчитывая точки на графике от начала координат, мы можем определить их точные значения и взаимное положение.
Определение

Ордината обозначается как y-координата, а абсцисса - как x-координата. Эти термины используются для обозначения соответствующих осей на графике.
Ордината и абсцисса имеют свои противоположности. Если на графике точка находится выше (выше абсциссы) оси ординат, то ее y-координата будет положительной. Если точка находится ниже (ниже абсциссы) оси ординат, то ее y-координата будет отрицательной. То же самое касается и абсциссы: точка, находящаяся правее оси ординат, будет иметь положительную x-координату, а находящаяся левее - отрицательную.
Ордината и абсцисса вместе позволяют определить положение точки на графике и ее отношение к другим точкам. Эти координаты являются основой работы с декартовой системой координат, которая широко используется в математике, физике, экономике и других областях.
Графическое представление
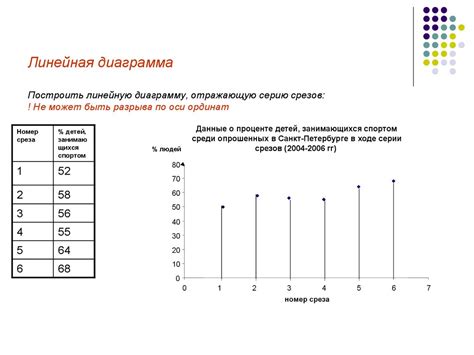
Ордината (также известная как вертикальная ось) - это ось, которая отображает значения зависимой переменной. На этой оси откладываются числовые значения, которые могут быть различного характера, включая цены, объемы, процентные изменения или любые другие числовые показатели. Однако, это не всегда так и ордината может нести и другую информацию, например, идентификаторы категорий или названия.
Абсцисса (также известная как горизонтальная ось) - это ось, которая отображает значения независимой переменной. На этой оси отображаются категории, переменные или другие структурированные данные, как правило, безразмерные.
График, таким образом, использует две оси, чтобы показать, как значения различных переменных взаимодействуют друг с другом. По мере того, как значения одной переменной изменяются вдоль абсциссы, они отображаются на соответствующей точке на ординате, позволяя наглядно представить, как одна переменная влияет на другую.
Понимание представления данных на графике с помощью осей ординаты и абсциссы позволяет анализировать данные, определять тренды, обнаруживать выбросы и выделять основные отношения между переменными.
Противоположность значений

Противоположность значений ординаты и абсциссы заключается в их направлении на графике. Если ордината представляет положительные и отрицательные значения сверху вниз, то абсцисса представляет положительные и отрицательные значения слева направо.
Таким образом, ордината и абсцисса являются противоположными в отношении направления значений на графике. Их пересечение в точке начала координат (0, 0) определяет нулевое значение для обеих осей.
Использование ординаты и абсциссы на графике позволяет визуализировать зависимость переменных и анализировать их изменения в разных направлениях. Вместе они образуют систему координат, которая является основой для построения графиков и решения математических задач.
Понимание связи
Ордината - это вертикальная ось координат. Она противоположна абсциссе, которая является горизонтальной осью координат. Ордината обозначается буквой y, а абсцисса - буквой x.
На графике ордината и абсцисса пересекаются в точке, которая называется началом координат. Эта точка имеет координаты (0, 0) и является отправной точкой для определения положения всех остальных точек на плоскости.
С помощью ординаты и абсциссы можно определить положение любой точки на графике. Каждая точка имеет свои координаты (x, y), где x - это значение на абсциссе, а y - значение на ординате.
| Ось | Направление |
|---|---|
| Ордината (y) | Вертикальное, вверх - положительное направление, вниз - отрицательное направление |
| Абсцисса (x) | Горизонтальное, вправо - положительное направление, влево - отрицательное направление |
Таким образом, ордината и абсцисса являются взаимообратными и противоположными значениями на графике. Они позволяют описывать положение точек на плоскости и строить различные геометрические фигуры.




