В математике периодической функцией называется функция, которая возвращается к своему исходному значению через определенный интервал времени или пространства. Это означает, что при заданном периоде функция демонстрирует повторяющееся поведение. Однако не все функции являются периодическими.
Определение периодической функции просто: функция f(x) называется периодической, если существует число T, такое что f(x+T) = f(x) для всех значений x. Число T называется периодом функции и отображает, через какой интервал функция возвращается к своему исходному значению.
Примеры периодических функций включают синусоиду (sin(x)) и косинусоиду (cos(x)), которые имеют период 2π и проходят через свои значения каждые 2π единиц времени или пространства. Другим примером является функция модуля (|x|), которая имеет период 2 и возвращает свое исходное значение каждые 2 единицы времени или пространства.
Что такое периодическая функция?

Для определения периодической функции необходимо найти такое число T, называемое периодом функции, что для любого x верно равенство f(x+T) = f(x). Если T - наименьшее положительное число, для которого выполняется это равенство, то оно называется основным периодом функции.
Примеры периодических функций включают гармонические функции, такие как синус и косинус, которые имеют период 2π, а также прямоугольные, треугольные и пилообразные волны.
Периодические функции широко используются в различных областях науки и техники, таких как телекоммуникации, электроника, музыка, оптика и др.
| Примеры периодических функций | Период |
|---|---|
| Синус | 2π |
| Косинус | 2π |
| Прямоугольная волна | T |
| Треугольная волна | 2T |
| Пилообразная волна | 2T |
Признаки периодической функции
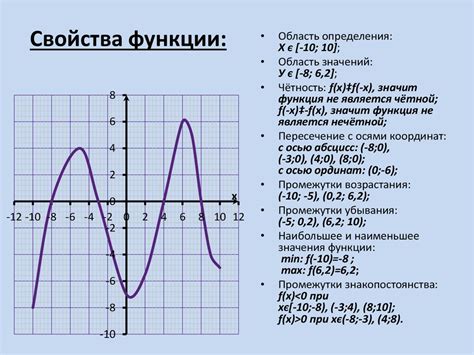
Периодическая функция имеет несколько характерных признаков, которые позволяют определить ее периодичность:
- Период: Основной характеристикой периодической функции является период, то есть интервал, через который функция повторяется. В математике период обозначают символом T. Если для всех x из области определения функции f(x) выполняется равенство f(x + T) = f(x), то функция считается периодической.
- Область определения: Для того чтобы функция была периодической, она должна быть определена на всей числовой прямой или на некотором интервале, который содержит период функции.
- Амплитуда: Амплитуда периодической функции – это разность между ее максимальным и минимальным значениями за один период.
- Фаза: Фаза периодической функции – это сдвиг функции по оси абсцисс относительно начала координат. Фаза может быть отрицательной или положительной, и определяется отношением точки сдвига к периоду функции.
Зная эти признаки, можно легко определить, является ли функция периодической, и привести примеры периодических функций, таких как синусоида, косинусоида, прямоугольные импульсы и др.
Примеры периодических функций
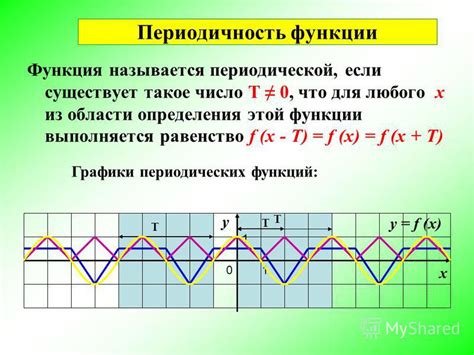
1. Синусоида (синус и косинус)
Самым известным и простым примером периодической функции является синусоида, которая представляет собой график синуса или косинуса. Синусоида повторяется с равными интервалами и имеет период, определяемый по формуле:
T = 2π/ω
где T - период функции, а ω - угловая частота.
2. Постоянная функция
Постоянная функция - это функция, которая принимает одно и то же значение на всем протяжении своего диапазона. Она также является периодической функцией с бесконечно большим периодом или периодом равным нулю.
3. Прямоугольный импульс
Прямоугольный импульс - это функция, которая принимает одно и то же значение внутри определенного интервала и равна нулю вне этого интервала. Прямоугольный импульс также является периодической функцией с периодом, равным ширине импульса.
4. Пилообразная функция
Пилообразная функция - это функция, которая линейно возрастает или убывает на определенном интервале, после чего резко меняет направление и снова повторяется. Данная функция также является периодической с периодом, равным длине интервала, на котором она повторяется.
Периодическая функция или константа: различия
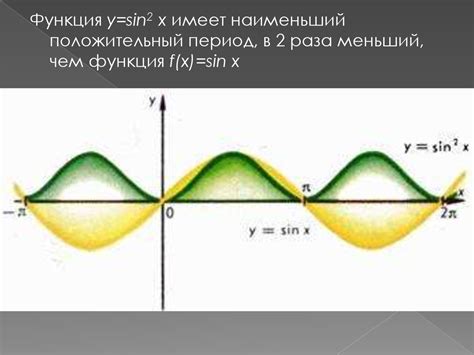
Периодическая функция - это функция, которая имеет период, то есть значение функции возвращается к своему начальному значению через определенные интервалы времени или значений аргумента. Другими словами, периодическая функция повторяет один и тот же график через равные промежутки времени или значений аргумента.
Константа - это значение, которое не меняется. Константа является функцией с постоянным значением в любой точке. Ее график представляет собой горизонтальную прямую, так как значение функции не зависит от значения аргумента.
Основное различие между периодической функцией и константой заключается в том, что периодическая функция имеет циклическую природу и повторяется через определенные интервалы времени или значений аргумента, в то время как константа остается постоянной независимо от значения аргумента.
Например, функция y = sin(x) является периодической функцией с периодом 2π, так как ее график повторяется через каждые 2π радиан. С другой стороны, функция y = 5 является константой, так как ее значение равно 5 независимо от значения аргумента x.
Таким образом, различие между периодической функцией и константой заключается в их поведении относительно изменения значения аргумента: периодическая функция циклически повторяет свой график, а константа имеет постоянное значение.
Связь периодических функций с графиками
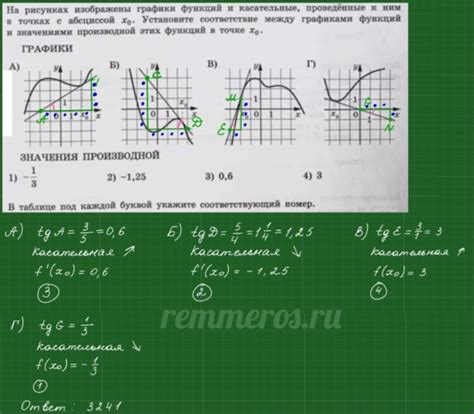
Например, рассмотрим график синусоидальной функции f(x) = sin(x):
| x | f(x) = sin(x) |
|---|---|
| 0 | 0 |
| π/4 | √2/2 |
| π/2 | 1 |
| 3π/4 | √2/2 |
| π | 0 |
| 5π/4 | -√2/2 |
| 3π/2 | -1 |
| 7π/4 | -√2/2 |
| 2π | 0 |
Из представленной таблицы видно, что функция f(x) = sin(x) имеет период равный 2π, так как значения функции повторяются с этим интервалом. Графически график синусоиды будет выглядеть как "волна", повторяющаяся синусоида за синусоидой.
Таким образом, представление графиков периодических функций в виде таблицы позволяет легко определить их периодичность и понять, как они повторяются на протяжении всей числовой оси.
Периодическая функция в математических моделях
Периодические функции широко применяются в различных областях науки и техники. Например, в физике они используются для моделирования колебаний и волновых процессов. Многие природные явления, такие как сезонные изменения, дневные и ночные циклы, имеют периодическую природу и могут быть описаны периодическими функциями.
В математических моделях периодические функции часто применяются для описания повторяющихся паттернов или закономерностей. Они позволяют анализировать и предсказывать поведение систем на основе их периодической структуры. Например, периодические функции используются в финансовой математике для предсказания ценовых колебаний на рынке.
Примером периодической функции может служить синусоида. Эта функция повторяет свое значение через определенный интервал времени или угла. Синусоида имеет период 2π и амплитуду, которая может быть изменена для создания различных форм колебаний.
В заключение, периодическая функция является важным инструментом для анализа и моделирования различных явлений. Ее использование позволяет описывать повторяющиеся паттерны и предсказывать поведение систем. Периодические функции находят применение в физике, технике, экономике и других областях науки и техники.




