Прямая пересечения плоскостей – это линия, которая одновременно лежит в двух плоскостях и является их общим пересечением. Точки этой линии принадлежат обеим плоскостям и удовлетворяют их уравнениям. Определение прямой пересечения плоскостей важно в геометрии и аналитической геометрии, а также во многих её приложениях, таких как механика, архитектура и физика.
Процесс определения прямой пересечения плоскостей состоит из нескольких шагов. Во-первых, необходимо найти направляющий вектор для каждой плоскости. Это можно сделать, найдя произведение векторов, лежащих в плоскости. Затем, следует взять векторное произведение направляющих векторов плоскостей, чтобы получить вектор, параллельный прямой пересечения плоскостей.
Например, если у нас есть две плоскости с уравнениями 2x + 3y - z = 4 и x + 2y + 2z = 5, мы можем найти направляющие векторы для этих плоскостей и взять их векторное произведение, чтобы определить направляющий вектор прямой пересечения.
Затем, нужно найти точку, через которую проходит прямая пересечения плоскостей. Для этого можно решить систему уравнений, состоящую из уравнений плоскостей, и найти координаты общей точки пересечения. Таким образом, мы получим параметрическое уравнение прямой пересечения плоскостей, которое позволяет нам легко описывать её положение в пространстве.
Прямая пересечения плоскостей: что это такое и как она определяется?
Для определения прямой пересечения плоскостей необходимо рассмотреть уравнения этих плоскостей. В общем случае, уравнение плоскости имеет вид:
| Аx + By + Cz + D = 0 |
Здесь A, B и C – коэффициенты, определяющие нормальный вектор плоскости, а D – свободный член.
Если заданы две плоскости с уравнениями:
| A1x + B1y + C1z + D1 = 0 |
| A2x + B2y + C2z + D2 = 0 |
То прямая пересечения плоскостей определяется следующим образом:
- Найдем нормальные векторы плоскостей. Для первой плоскости это будет вектор (A1, B1, C1), а для второй – вектор (A2, B2, C2).
- Найдем вектор, перпендикулярный обоим нормальным векторам. Это можно сделать, взяв векторное произведение двух нормальных векторов.
- Для полученного вектора найдем точку, через которую пройдет прямая пересечения. Для этого решим систему уравнений, составленных из уравнений плоскостей.
- Используя точку и направляющий вектор, найденные на предыдущих шагах, составим параметрическое уравнение прямой.
Таким образом, прямая пересечения плоскостей определяется с помощью уравнений плоскостей и метода векторного анализа.
Плоскость и ее определение

Плоскость может быть задана различными способами. Одним из наиболее распространенных способов задания плоскости является использование ее нормального вектора и точки, через которую она проходит. Нормальный вектор плоскости - это вектор, перпендикулярный к плоскости и указывающий в каком-то направлении.
Для определения плоскости необходимо указать как минимум три точки, через которые она проходит. Для определения однозначной плоскости достаточно указать еще одну точку, не лежащую на прямой, образующейся при пересечении плоскости с другой плоскостью или прямой.
Зная координаты точек и вектор, определяющий плоскость, можно определить уравнение плоскости. В общем случае уравнение плоскости имеет вид:
Ax + By + Cz + D = 0
где A, B и C - коэффициенты, определяющие нормальный вектор плоскости, D - свободный член.
Таким образом, плоскость является важным понятием в математике и имеет множество приложений в различных областях, таких как геометрия, физика, аэродинамика и графика.
Прямая и ее свойства
Свойства прямой включают:
- Прямая проходит через две точки. Для определения прямой необходимо знать координаты двух точек, через которые она проходит.
- Прямая имеет направление. Оно может быть задано выбором любого вектора, коллинеарного прямой.
- Прямая имеет наклон. Он может быть определен с помощью угла между прямой и одной из координатных плоскостей.
- Прямая может быть параллельна или пересекать другую прямую. В зависимости от положения их углов и направлений, прямые могут быть параллельными, пересекающимися или скрещивающимися.
Прямая – основной элемент геометрии и находит применение во многих областях, таких как архитектура, машиностроение и геодезия.
Пересечение плоскостей: что это значит?
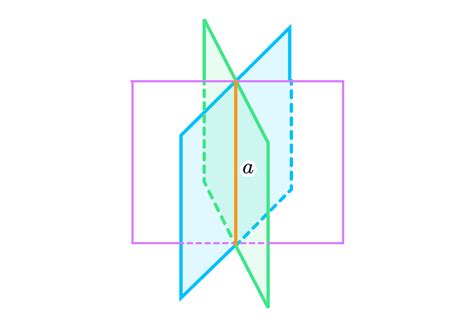
Плоскости в трехмерном пространстве могут пересекаться по-разному. Если две плоскости имеют точку пересечения, то они пересекаются в одной точке. Если две плоскости имеют общую прямую линию, то они пересекаются по этой линии.
Чтобы определить пересечение двух плоскостей, нужно учесть их уравнения. Уравнение каждой плоскости описывает все точки, которые принадлежат этой плоскости, а пересечение плоскостей – это все точки, которые одновременно принадлежат обеим плоскостям.
Пересечение плоскостей является важным понятием в геометрии и математике. Оно используется во множестве практических задач и приложений, включая строительство, инженерию и графический дизайн.
Прямая пересечения плоскостей: определение и условия
Прямая пересечения плоскостей представляет собой линию, на которой лежат точки, принадлежащие одновременно двум плоскостям. Эта линия может быть тривиальной, состоящей из одной точки, или натянутой между двумя точками. Чтобы определить такую прямую, необходимо выполнение определенных условий, о которых пойдет речь далее.
Если две плоскости имеют общую прямую пересечения, это означает, что они не параллельны друг другу и не совпадают. Для того чтобы определить такую прямую пересечения, необходимо, чтобы общая прямая лежала в каждой из плоскостей. Другими словами, все точки этой прямой должны удовлетворять уравнениям обеих плоскостей.
Если даны две плоскости, заданные уравнениями Ax + By + Cz + D1 = 0 и Ex + Fy + Gz + D2 = 0, где A, B, C, D1, E, F, G и D2 - известные коэффициенты, то их прямая пересечения может быть найдена следующим образом:
- Решить систему уравнений A1x + B1y + C1z + D1 = 0 и A2x + B2y + C2z + D2 = 0, где A1 = A, B1 = B, C1 = C, D1 = -D1, A2 = E, B2 = F, C2 = G, D2 = -D2. Полученное решение представляет собой направляющий вектор линии, поскольку оно удовлетворяет уравнениям обеих плоскостей.
- Выбрать любую точку на линии, например, можно положить x = 0 и решить уравнение y = (-C1z - D1) / B1, где z - любое допустимое значение. Это позволит нам получить начальную точку на линии.
Таким образом, прямая пересечения плоскостей может быть определена с помощью решения системы уравнений, заданных уравнениями плоскостей, и выбором точки на этой прямой. Она будет проходить через эту точку и иметь направление указанное направляющим вектором.
Задача о прямой пересечения плоскостей: примеры решения
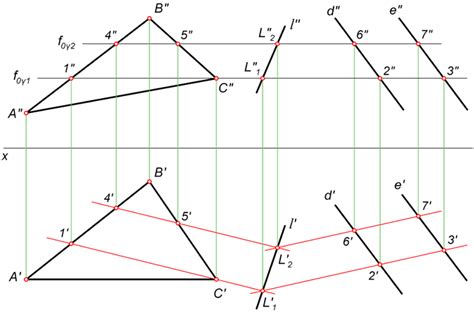
Метод 1: Аналитический метод
Для начала, задачу можно решить аналитически, используя систему уравнений, описывающую две плоскости. В этом случае необходимо найти параметрическое уравнение прямой, которая будет являться их пересечением. Процесс решения можно разбить на несколько шагов:
- Записать уравнения плоскостей в общем виде, определить неизвестные коэффициенты.
- Преобразовать систему уравнений таким образом, чтобы избавиться от одной переменной.
- Используя параметрическое уравнение прямой, найти координаты точек ее пересечения с плоскостями.
В результате получим координаты точек прямой пересечения плоскостей.
Метод 2: Геометрический метод
Второй подход к решению задачи о прямой пересечения плоскостей основан на геометрическом подходе. В этом случае необходимо построить плоскости и оси, отобразить их на плоскости, чтобы найти точки пересечения. Для этого можно использовать следующие шаги:
- На бумаге или в графическом редакторе нарисовать плоскости, используя их уравнения.
- Построить оси координат и отметить на них точки, соответствующие координатам плоскостей.
- Найти точки, где пересекаются оси и плоскости.
Таким образом, мы определим точки пересечения и сможем построить прямую, являющуюся их общим пересечением.
Геометрический смысл прямой пересечения плоскостей
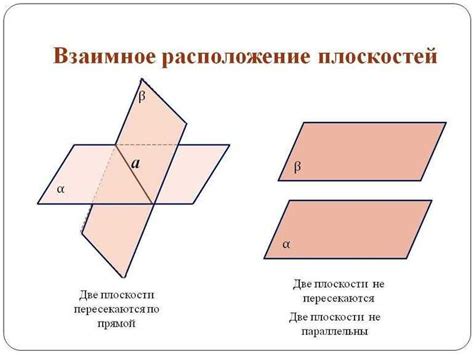
Прямая пересечения плоскостей может иметь различные характеристики в зависимости от угла, под которым плоскости пересекаются. Например, если плоскости пересекаются под прямым углом, прямая пересечения будет вертикальная и проходить через центры обеих плоскостей. Если плоскости пересекаются под острым углом, прямая пересечения будет наклонной и не будет проходить через центры плоскостей.
Прямая пересечения плоскостей имеет важное значение в геометрии и находит применение в различных областях, таких как инженерия, архитектура, строительство и т.д. Зная прямую пересечения плоскостей, можно определить точки пересечения различных геометрических объектов, провести трассировку линий и определить расстояние между различными объектами.
Практическое применение прямой пересечения плоскостей
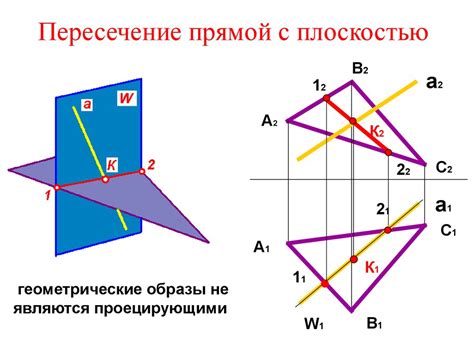
Прямая пересечения плоскостей находит широкое применение в различных областях науки и инженерии. Вот некоторые примеры ее практического использования:
1. Графическое моделирование Прямая пересечения плоскостей используется при создании трехмерных моделей объектов в компьютерной графике. Это позволяет определить точки, в которых плоскости пересекаются, а также строить линии и формы, основываясь на этих пересечениях. Это позволяет создавать реалистичные и привлекательные визуальные эффекты. | 2. Архитектура и строительство В архитектуре и строительстве прямая пересечения плоскостей используется для определения точек пересечения стен, потолков и полов. Это позволяет строить правильные и устойчивые конструкции, а также определять точки взаимодействия различных элементов здания. |
3. Машиностроение Прямая пересечения плоскостей применяется в машиностроении для определения допустимых траекторий движения частей механизмов. Это помогает избежать коллизий и обеспечивает безопасность работы машин и устройств. | 4. Расчеты в физике Прямая пересечения плоскостей используется в физике для решения задач, связанных с траекториями движения тел. Она позволяет определить точки пересечения движущихся объектов и предсказать их будущее положение в пространстве. |
Это лишь некоторые примеры практического применения прямой пересечения плоскостей. Благодаря своей универсальности и точности, она находит применение во многих других областях, где необходимо анализировать пересечение плоскостей и определять точки и линии в пространстве.




