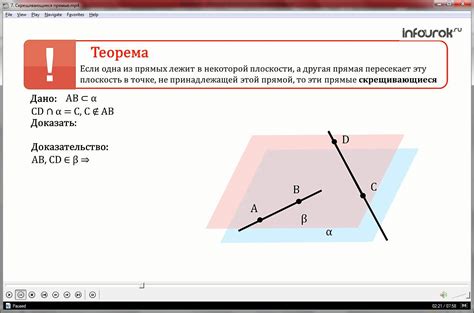
Скрещивающиеся прямые – это понятие из евклидовой геометрии, которое описывает взаимное положение двух прямых. Если две прямые не лежат на одной плоскости и имеют только одну общую точку, то они являются скрещивающимися. Это означает, что они пересекаются, образуя угол и создавая специальное взаимное расположение между собой.
Скрещивающиеся прямые оказываются важным понятием в геометрии, так как они являются основой для понимания пересечения прямых, углов, плоскостей и других элементов геометрических фигур. Они используются в различных областях, включая инженерию, архитектуру, физику и многие другие.
Например, скрещивающиеся прямые могут быть использованы для определения угла между двумя плоскостями или для построения трехмерной координатной системы. Они позволяют нам лучше понять пространственные отношения и создавать точные модели и конструкции.
В заключение, скрещивающиеся прямые – это основное понятие геометрии, которое описывает взаимное положение двух прямых в трехмерном пространстве. Они позволяют нам визуализировать и понимать геометрические фигуры и создавать точные модели. Знание этого понятия полезно для различных профессиональных и технических областей, где необходимо работать с трехмерными пространствами и углами.
Что такое скрещивающиеся прямые
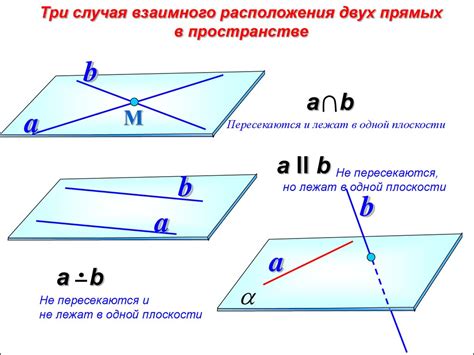
Когда две прямые скрещиваются, они образуют угол в точке пересечения. Такой угол называется углом пересечения. Угол пересечения может быть остроугольным, прямым или тупоугольным, в зависимости от того, какие прямые скрещиваются.
Примеры скрещивающихся прямых можно найти в различных ситуациях в повседневной жизни. Например, две дороги, которые пересекаются в перекрестке, образуют скрещивающиеся прямые. Также скрещивающиеся прямые можно обнаружить на плоскости графика или геометрической фигуры.
Понимание понятия скрещивающихся прямых полезно для решения задач, связанных с геометрией, и может быть использовано для анализа и определения различных свойств и отношений между прямыми.
Определение скрещивающихся прямых

Угол пересечения скрещивающихся прямых может быть как острый, так и тупой. Если угол равен 90 градусам, то такие прямые называются перпендикулярными. Если угол превышает 90 градусов, то прямые называются отрицательно перпендикулярными.
Примером скрещивающихся прямых может служить буква "X". В этом случае, каждая прямая, образующая букву "X", будет скрещиваться с другой прямой в точке пересечения углов.
Скрещивающиеся прямые имеют важное значение в геометрии и используются при решении различных задач и построений.
Примеры скрещивающихся прямых
- Пересечение двух возрастающих прямых: например, прямая линия, идущая вверх с угловым коэффициентом 2, и прямая линия, идущая вверх с угловым коэффициентом 1.5, будут скрещиваться в точке пересечения.
- Пересечение двух убывающих прямых: например, прямая линия, идущая вниз с угловым коэффициентом -2, и прямая линия, идущая вниз с угловым коэффициентом -3, будут скрещиваться в точке пересечения.
- Пересечение прямых с разными угловыми коэффициентами: например, прямая линия, идущая вверх с угловым коэффициентом 2, и прямая линия, идущая вниз с угловым коэффициентом -1, будут скрещиваться в точке пересечения.
Значение скрещивающихся прямых
Основное значение скрещивающихся прямых заключается в том, что они образуют точку пересечения. Эта точка, в которой прямые пересекаются, называется точкой пересечения. Точка пересечения – это уникальная точка на плоскости, которая определена только для данных двух прямых..
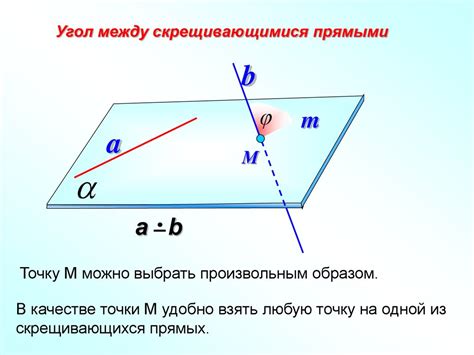
Скрещивающиеся прямые также используются для определения углов между ними. Угол между скрещивающимися прямыми определяется как угол между положительным направлением одной прямой и другой прямой, выходящей из точки пересечения. Угол между скрещивающимися прямыми может быть острый, прямой или тупой, в зависимости от их взаимного положения.
Примером скрещивающихся прямых могут служить пересекающиеся улицы на городской карте. Если две улицы пересекаются и не идут параллельно друг другу, то отрезок, где они пересекаются, будет скрещивающимся отрезком прямой линии. Также скрещивающиеся прямые можно наблюдать на перекрестках железнодорожных путей или на картах координатных систем.




