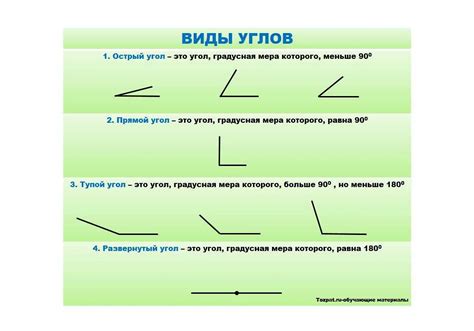
Угол - это фигура, образованная двумя лучами, которые обычно имеют одну и ту же начальную точку, называемую вершиной. В геометрии существует множество типов углов, и одним из наиболее важных и интересных являются углы, которые являются взаимно перпендикулярными.
Углы говорятся взаимно перпендикулярными, когда они образуют перпендикулярные линии или отрезки. Перпендикулярные линии пересекаются под прямым углом, то есть углом в 90 градусов. Это является одним из основных свойств перпендикулярности, которое делает такие углы особенно важными в геометрии.
Важным свойством взаимно перпендикулярных углов является то, что сумма их мер всегда равна 180 градусам. Таким образом, если один угол равен 90 градусам, то второй угол также равен 90 градусам.
Примерами взаимно перпендикулярных углов могут служить все четверть круга, состоящие из двух соседних углов, каждый из которых равен 90 градусам. Также взаимно перпендикулярные углы могут быть образованы линией, пересекающей другую линию под прямым углом. Это свойство находит широкое применение в различных областях, включая архитектуру, инженерию и дизайн.
Взаимно перпендикулярные углы: понятие и определение

В геометрии существуют особые углы, которые называются взаимно перпендикулярными углами. Для того чтобы понять, что такое взаимно перпендикулярные углы, нужно разобраться с понятием перпендикулярности.
Перпендикулярные линии или отрезки – это линии или отрезки, которые пересекаются между собой, образуя прямой угол. А прямой угол равен 90 градусам, что означает, что перпендикулярные линии образуют прямой угол.
Углы могут быть отрицательными или положительными, в зависимости от направления вращения от одного отрезка до другого. Взаимно перпендикулярные углы – это два угла, каждый из которых перпендикулярен другому.
Основными свойствами взаимно перпендикулярных углов являются:
- Сумма взаимно перпендикулярных углов равна 90 градусам.
- Углы, составляющие взаимно перпендикулярные углы, являются смежными.
- Если один угол взаимно перпендикулярен другому, то их комплиментарные углы также будут перпендикулярны друг другу.
Примером взаимно перпендикулярных углов может служить пересечение двух перпендикулярных линий. При таком пересечении образуется четыре угла, два из которых будут взаимно перпендикулярными.
Свойства взаимно перпендикулярных углов
Взаимно перпендикулярные углы обладают следующими свойствами:
| Свойство | Описание |
| 1 | Сумма взаимно перпендикулярных углов равна 90 градусам. |
| 2 | Взаимно перпендикулярные углы дополняют друг друга. |
| 3 | Если угол A перпендикулярен углу B, то угол B также перпендикулярен углу A. |
| 4 | Взаимно перпендикулярные углы могут быть обозначены как A ⊥ B. |
Пример:
На рисунке видно два взаимно перпендикулярных угла А и В. Угол A имеет размер 30 градусов, следовательно, угол B равен 60 градусам.
Из свойства 1 следует, что 30° + 60° = 90°, что подтверждает правильность определения взаимно перпендикулярных углов.
Свойство №1: Углы равны между собой

Перпендикулярные углы имеют ряд свойств, которые определяют их особенности и характеристики.
Одно из таких свойств заключается в том, что все перпендикулярные углы равны между собой.
Если две прямые линии пересекаются или образуют перпендикулярный угол, то все углы, образованные этим пересечением или перпендикулярным углом, будут равны. Это означает, что углы, расположенные по разные стороны пересекающихся прямых, будут иметь одинаковую величину.
Например, если две прямые линии AB и CD пересекаются в точке O и образуют перпендикулярные углы AOC и BOD, то эти углы будут равны друг другу: AOC = BOD.
Свойство равенства перпендикулярных углов позволяет делать определенные выводы и решать задачи, связанные с геометрией. Например, если мы знаем значение одного из перпендикулярных углов, то мы можем найти значение остальных углов, используя это свойство.
Свойство №2: Сумма взаимно перпендикулярных углов равна 90 градусам

Для наглядности рассмотрим пример. Представим, что у нас есть две прямые, A и B, которые пересекаются. Угол между этими прямыми, обозначенный как угол 1, и угол, образованный пересечением этих прямых, обозначенный как угол 2, являются взаимно перпендикулярными.
Согласно свойству №2, сумма углов 1 и 2 будет равна 90 градусам. Это свойство может быть объяснено по теореме о вертикальных углах: если две прямые перпендикулярны, то все вертикальные углы, образованные пересекающими прямыми, будут равными.
Таким образом, сумма углов 1 и 2, образованных пересечением перпендикулярных прямых, будет составлять 90 градусов. Это свойство является одним из основных свойств взаимно перпендикулярных углов и часто используется в геометрических вычислениях и построениях.
Свойство №3: Взаимно перпендикулярные углы образуют "L"-образные фигуры

"L"-образные фигуры встречаются в различных ситуациях и предметах повседневной жизни. Например, в углах комнат, зданий, мебели, конструкций и других объектах. Это свойство взаимно перпендикулярных углов позволяет упорядочить пространство и создать структуру, которая помогает нам понимать и организовывать окружающий нас мир.
"L"-образные фигуры имеют множество полезных свойств. Например, они могут использоваться для строительства прямых и устойчивых конструкций, таких как стены и фундаменты зданий. Также "L"-образные фигуры позволяют определить границы, разделить пространство на зоны и облегчить навигацию.
Взаимно перпендикулярные углы, образующие "L"-образные фигуры, широко применяются в геометрии и архитектуре. Они являются основой для различных конструкций и позволяют создавать устойчивые и симметричные формы.
Примеры взаимно перпендикулярных углов
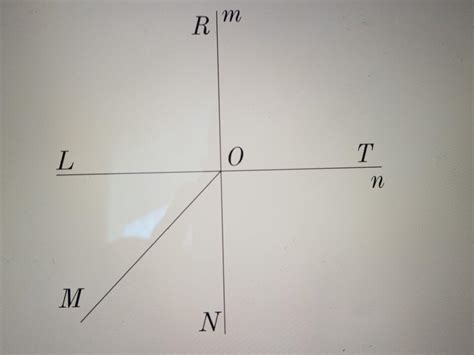
Пример 1:
Дан квадрат ABCD. Прямые AB и CD пересекаются в точке E. Углы AED и BEC являются взаимно перпендикулярными углами.
Пример 2:
Рассмотрим прямоугольник PQRS. Прямые PS и QR пересекаются в точке T. Углы STQ и TRP являются взаимно перпендикулярными углами.
Пример 3:
В треугольнике XYZ проведены высоты ZM и YN. Углы MYZ и ZNX являются взаимно перпендикулярными углами.
Таким образом, взаимно перпендикулярные углы встречаются в различных геометрических фигурах и имеют важное значение при решении задач по геометрии.
Пример №1: Углы в прямоугольном треугольнике
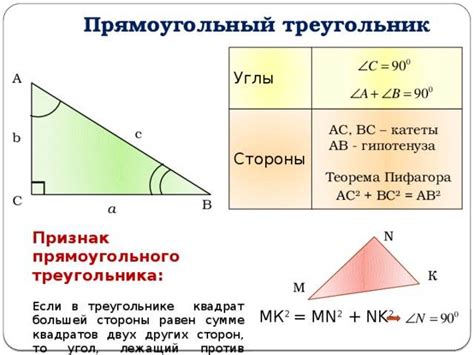
Один из таких углов - это прямой угол, который образуется гипотенузой и одним из катетов треугольника. Этот угол всегда равен 90 градусам и является основной характеристикой прямоугольного треугольника.
Другие два угла в прямоугольном треугольнике обычно называются острыми углами. Они всегда взаимно перпендикулярны и дополняют друг друга до прямого угла.
Например, если один из острых углов равен 30 градусам, то другой острый угол будет равен 60 градусам. Эти углы вместе образуют прямой угол в 90 градусов.
Таким образом, в прямоугольном треугольнике существуют углы, которые взаимно перпендикулярны и дополняют друг друга до прямого угла. Это является одним из основных свойств такого треугольника.
Пример №2: Углы в соответствующих углов

В данном примере мы рассмотрим углы в соответствующих углах. Если мы имеем две пары взаимно перпендикулярных прямых, то углы, образованные этими прямыми, называются соответствующими углами. Они находятся на одной стороне каждой из пересекаемых прямых и находятся от одной из прямых до другой параллельной прямой.
Свойства углов в соответствующих углах:
- Углы в соответствующих углах равны между собой. Если один угол равен 90 градусам, то и второй угол будет равен 90 градусам.
- Углы в соответствующих углах находятся по разные стороны пересекаемой прямой. Они образуют пару углов с двумя прямыми, пересекающими попарно пересекаемые прямые.
Например, рассмотрим две пересекаемые прямые AB и CD, перпендикулярные прямым EF и GH соответственно. Углы FAB и CGH являются соответствующими углами, так как они находятся на одной стороне пересекаемых прямых, между прямыми EF и GH. Из свойств следует, что эти углы будут равными.
Пример №3: Углы на пересечении двух прямых

Рассмотрим две пересекающиеся прямые AB и CD. В точке их пересечения образуются четыре угла:
- Угол АВС (или ВСА)
- Угол АСD (или CDA)
- Угол ВСB (или CBV)
- Угол АСВ (или CBA)
Углы АВС и ВСВ являются смежными и дополняют друг друга до 180 градусов:
- АВС + ВСВ = 180°
Также углы, лежащие на противоположных сторонах пересекаемых прямых, образуют пары взаимно перпендикулярных углов:
- АВС и АСD являются взаимно перпендикулярными углами
- ВСВ и ВСB являются взаимно перпендикулярными углами
- АВС и ВСВ являются взаимно перпендикулярными углами
- АСD и ВСB являются взаимно перпендикулярными углами
Эта особенность углов на пересечении двух прямых играет важную роль в геометрии и находит применение в различных конструкциях и вычислениях.




