Что значит возрастает или убывает линейная функция

Линейные функции являются одним из основных понятий в математике. Они используются для описания зависимости между двумя переменными. Одним из важнейших свойств линейных функций является их возрастание или убывание.

Как же определить, что линейная функция возрастает или убывает? Существует несколько простых принципов, которые помогут разобраться в этом вопросе. Во-первых, нужно определить, как меняются значения функции при увеличении или уменьшении аргумента. Если значения функции увеличиваются при увеличении аргумента, то говорят, что функция возрастает. Если значения функции убывают при увеличении аргумента, то говорят, что функция убывает.

Ещё одним способом определить возрастание или убывание линейной функции является анализ её графика. Если график функции имеет положительный наклон, то функция возрастает. Если график функции имеет отрицательный наклон, то функция убывает. Наклон графика можно определить, посмотрев на угол, под которым прямая пересекает ось абсцисс.

Например, рассмотрим линейную функцию y = 2x + 1. Определим её возрастание или убывание. При увеличении аргумента x на единицу значения функции возрастают на 2. Таким образом, можно сделать вывод, что функция возрастает. При построении графика этой функции мы увидим, что прямая имеет положительный наклон, подтверждая наше предположение.

Как узнать направление линейной функции: понимание и примеры

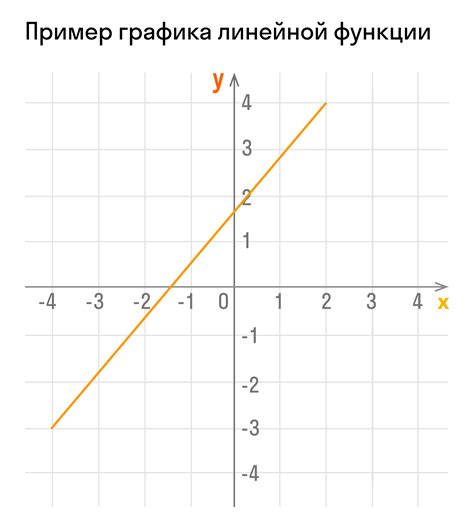
Возрастание и убывание – это два основных направления, которые может иметь линейная функция. Они определяются по значению коэффициента k. Если k больше нуля, то функция возрастает, а если k меньше нуля, то функция убывает.

Пример 1:

Рассмотрим функцию y = 2x + 1. Коэффициент k равен 2, что больше нуля. Это означает, что функция возрастает. При увеличении значения x, значение y также будет увеличиваться.

Пример 2:

Теперь рассмотрим функцию y = -3x - 2. Коэффициент k равен -3, что меньше нуля. Следовательно, эта функция убывает. При увеличении значения x, значение y будет уменьшаться.

Итак, чтобы определить направление линейной функции, нужно:

1. Найти значение коэффициента k в уравнении функции.
2. Сравнить значение k с нулем.
3. Если k больше нуля, то функция возрастает.
4. Если k меньше нуля, то функция убывает.

Понятие линейной функции и основные свойства

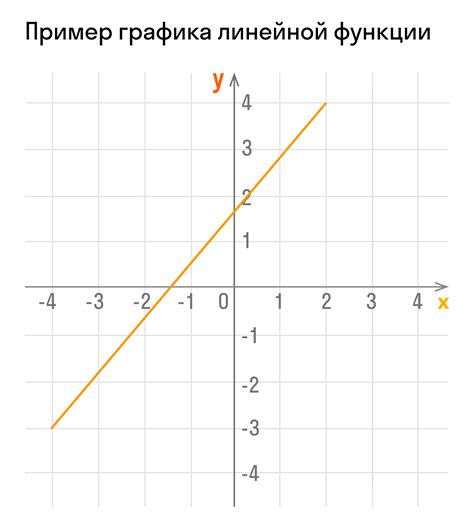
Основные свойства линейной функции:

• Линейная функция представляет собой уравнение вида y = kx + b, где k и b - коэффициенты, х - независимая переменная, y - зависимая переменная. Коэффициент k определяет наклон прямой, а коэффициент b - точку пересечения с осью у.
• Если коэффициент k положительный, то функция является возрастающей. Это означает, что при увеличении значения независимой переменной x, значение зависимой переменной y также увеличится.
• Если коэффициент k отрицательный, то функция является убывающей. Это означает, что при увеличении значения независимой переменной x, значение зависимой переменной уменьшится.
• Если коэффициент k равен нулю, то функция является постоянной. Это означает, что значение зависимой переменной y не зависит от значения независимой переменной x и остается неизменным.

Например, функция y = 2x + 3 является возрастающей, так как коэффициент k равен положительному числу 2. График этой функции будет прямой, и ее значение будет увеличиваться при увеличении значения x.

Как определить возрастание линейной функции

Для определения возрастания линейной функции необходимо анализировать знак её коэффициента при переменной, которая увеличивается. Если коэффициент при этой переменной положителен, то функция возрастает. Если коэффициент отрицателен, то функция убывает.

Можно использовать следующий алгоритм для определения возрастания линейной функции:

1. Записать уравнение линейной функции в виде y = kx + b, где k - коэффициент при переменной x, а b - свободный член.
2. Если k > 0, то функция возрастает.
3. Если k

Например, рассмотрим линейную функцию y = 2x + 5. Здесь коэффициент k равен 2, что больше нуля. Следовательно, данная функция возрастает.

Таким образом, зная знак коэффициента при переменной x, можно определить, является ли линейная функция возрастающей или убывающей. Это знание важно для понимания поведения функции и её графика.

Как определить убывание линейной функции

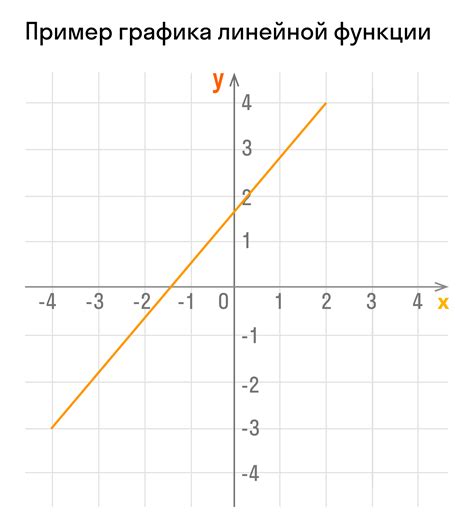
Для определения коэффициента наклона необходимо использовать формулу:

м = (y₂ - y₁) / (x₂ - x₁),

где (x₁, y₁) и (x₂, y₂) это две точки на графике функции.

Если меньше нуля, то линейная функция убывает. Если равен нулю, то функция является постоянной (горизонтальной прямой), а если больше нуля, то функция возрастает.

Пример:

Рассмотрим линейную функцию y = 2x - 3. Для определения ее наклона выберем две точки (1, -1) и (3, 3). Применяя формулу, получим:

м = (3 - (-1)) / (3 - 1) = 4 / 2 = 2.

Коэффициент наклона равен 2, что больше нуля. Значит, данная линейная функция возрастает.