Целые решения системы неравенств являются решениями, которые удовлетворяют условиям системы, принимая только целочисленные значения. Такие решения являются важными в математике и практически во всех областях науки и техники.
Целые решения системы неравенств могут использоваться для моделирования различных ситуаций, например, оптимизации производственных и логистических процессов, планирования и расписания задач. Они позволяют найти наилучшие решения с учетом ограничений и условий задачи.
Целые решения системы неравенств также важны при решении проблем комбинаторики, когда требуется подсчитать или перебрать все варианты комбинаций с определенными ограничениями.
Например, если мы рассматриваем систему неравенств, ограничивающих количество ресурсов, которые можно использовать, целочисленные решения позволяют найти оптимальные значения для использования ресурсов, учитывая их ограниченность.
Выводы, полученные в результате поиска целых решений системы неравенств, могут помочь в принятии важных решений, оптимизации процессов и планировании действий в различных областях деятельности.
Определение и примеры
Рассмотрим пример системы неравенств:
- 2x + y ≥ 5
- x + 3y ≤ 10
- x ≥ 0
- y ≥ 0
Целое решение данной системы может быть найдено путем подстановки различных значений для переменных x и y и проверки, удовлетворяет ли неравенства. В данном случае, целые решения могут быть, например:
- x = 2, y = 1
- x = 4, y = 0
- x = 3, y = 2
Эти значения удовлетворяют всем неравенствам в системе, так как при подстановке они приводят к верным неравенствам. Целые решения играют важную роль в различных областях, таких как математика, экономика, инженерия и других. Они позволяют находить оптимальные или допустимые значения переменных для достижения конкретных целей или ограничений.
Определение целых решений системы неравенств

В системе неравенств могут присутствовать как знаки "" (больше) вместе с различными математическими операциями. Целые числа - это числа без десятичной части (целые числа без знака) и не должны быть дробными или числами с плавающей запятой.
Важно искать и учитывать целые решения системы неравенств, так как они позволяют нам найти все возможные целочисленные значения переменных, которые удовлетворяют системе. Это может быть полезно, например, при решении задач по оптимизации или при анализе возможных вариантов.
Целые решения системы неравенств могут быть найдены с помощью различных методов, таких как графическое представление, аналитическое решение или использование алгоритмов. Важно учесть все условия и ограничения системы, чтобы найти корректные целочисленные решения.
Примеры систем неравенств с целыми решениями

Целые решения систем неравенств играют важную роль во многих областях математики и приложений. Они позволяют нам найти конкретные значения переменных, удовлетворяющие заданным ограничениям, и решить различные задачи.
Рассмотрим несколько примеров систем неравенств с целыми решениями:
| Пример | Система неравенств | Целые решения |
|---|---|---|
| 1 | 2x + 5y ≤ 10 | x = 0, y = 2; x = 1, y = 1; x = 2, y = 0 |
| 2 | 3x + 4y ≤ 12 | x = 0, y = 3; x = 1, y = 2; x = 2, y = 0 |
| 3 | x + y ≤ 5 | x = 0, y = 5; x = 1, y = 4; x = 2, y = 3; x = 3, y = 2; x = 4, y = 1; x = 5, y = 0 |
Во всех данных примерах системы неравенств содержат две переменные и ограничивающие условия, заданные неравенствами. Целые решения позволяют нам найти все возможные значения переменных, которые удовлетворяют заданным ограничениям.
Знание целых решений систем неравенств помогает в решении задач оптимизации, планирования и определении допустимых значений переменных, гарантирующих выполнение определенных условий.
Роль в математике

Целые решения системы неравенств позволяют нам определить набор всех целых чисел, которые удовлетворяют заданной системе неравенств. Это может быть полезно во многих прикладных задачах, где требуется определить диапазон возможных значений для переменных.
Целые решения системы неравенств также используются для изучения связей между различными неравенствами и их геометрическими интерпретациями. Например, они могут помочь нам определить области на координатной плоскости, в которых выполняются заданные условия.
Более того, целые решения системы неравенств могут быть использованы для доказательства различных математических утверждений и теорем. Они позволяют нам установить существование и количество решений для заданных условий.
В целом, целые решения системы неравенств играют важную роль в математике, предоставляя нам инструменты для анализа неравенств, установления связей между ними и решения различных математических задач.
Целые решения систем неравенств в алгебре

Системы неравенств в алгебре часто задачаются для определения диапазона значений переменных, при которых система выполняется. Целые решения систем неравенств играют важную роль в алгебре, потому что они позволяют найти все целочисленные значения переменных, удовлетворяющие системе.
Целые решения системы неравенств определяются как значения переменных, которые являются целыми числами и удовлетворяют всем неравенствам в системе. Например, система неравенств может иметь вид:
2x - y ≤ 4
3x + 2y > 7
Целые решения этой системы неравенств можно найти, перебирая все возможные целочисленные значения переменных x и y и проверяя их на удовлетворение обоим неравенствам. Таким образом, целые решения системы неравенств представляют собой целочисленные точки в координатной плоскости, которые удовлетворяют всем неравенствам.
Целые решения системы неравенств в алгебре имеют практическое значение при решении задач, связанных с определением диапазона значений переменных. Кроме того, они могут быть полезны для нахождения оптимальных решений при решении оптимизационных задач.
В заключение, целые решения систем неравенств играют важную роль в алгебре, позволяя найти все целочисленные значения переменных, которые удовлетворяют системе неравенств. Они имеют практическое значение и могут быть полезны при решении различных задач в алгебре и оптимизации.
Целые решения систем неравенств в геометрии
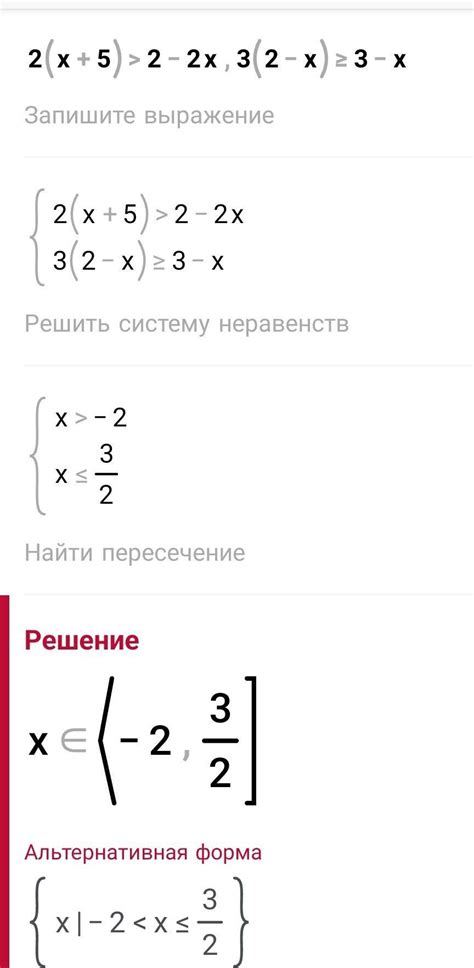
Целые решения системы неравенств - это значения переменных, которые удовлетворяют всем неравенствам системы и являются целыми числами. Например, система неравенств может выглядеть так:
2x + 3y ≤ 10
x - y ≥ 2
Целые решения этой системы будут значения переменных x и y, которые удовлетворяют данным неравенствам и являются целыми числами. Например, (2, 1) является одним из целых решений этой системы, так как 2*2 + 3*1 ≤ 10 и 2 - 1 ≥ 2.
Целые решения систем неравенств в геометрии широко применяются для нахождения оптимальных значений в различных задачах. Например, можно использовать целые решения для определения оптимального количества производимых товаров, оптимального размещения объектов на плоскости или оптимальной цены продукта.
Также целые решения систем неравенств позволяют находить точки пересечения графиков функций, что важно при решении графических задач. При построении графика системы неравенств, целые решения представляются в виде точек на плоскости, что позволяет визуализировать их и анализировать.
В целом, целые решения систем неравенств в геометрии играют важную роль в нахождении оптимальных значений и решении графических задач. Они помогают нам понять, какие значения переменных удовлетворяют неравенствам и являются целыми числами, что позволяет нам найти оптимальное решение и принять соответствующие решения в реальной жизни.
Практическое применение

- Линейное программирование: В задачах линейного программирования требуется определить максимальное или минимальное значение линейной функции от нескольких переменных при условии, что эти переменные удовлетворяют некоторым неравенствам. Целые решения системы неравенств могут помочь найти оптимальное решение, учитывая ограничения и требования задачи.
- Дискретная математика: Целые решения систем неравенств имеют важное значение при решении комбинаторных и дискретных задач. Например, задача о назначениях, пути в графе или раскраске карты могут быть сформулированы в терминах систем неравенств, где целые решения представляют оптимальные или допустимые решения.
- Распределение ресурсов: В экономике и управлении ресурсами целые решения систем неравенств играют важную роль при определении оптимального распределения ресурсов, таких как финансы, трудовые ресурсы или материалы. Целостные решения могут помочь снизить затраты или максимизировать прибыль, учитывая ограничения и требования деловых ситуаций.
- Проектирование и оптимизация: Целые решения систем неравенств могут быть использованы для оптимизации процессов и проектов, таких как планирование производства, оптимизация маршрутов или размещение объектов. Целые решения помогают учесть ограничения, такие как время, пропускная способность или стоимость, при принятии решений.
Все эти примеры демонстрируют важность целостных решений систем неравенств в различных сферах деятельности. Они позволяют находить оптимальные, допустимые или наилучшие решения, основываясь на условиях и ограничениях, заданных системой неравенств.




