Вектор – это математический объект, который обладает величиной и направлением. Вектор может быть выражен как комбинация других векторов. Однако для этого необходимо знать координаты этих векторов и их линейную независимость.
Выражение вектора через другие два вектора может быть полезным при решении различных задач в физике, геометрии и других областях. Оно позволяет упростить вычисления и получить более наглядное представление о векторах.
Для выражения вектора а через два вектора б и в необходимо найти такие числа x и y, что а = xб + yв. Векторы б и в должны быть линейно независимыми, то есть один вектор не должен быть множителем другого.
Пример: пусть имеются векторы а = (-3, 2) и б = (4, -1). Необходимо выразить вектор а через эти два вектора. Для этого найдем такие числа x и y, что а = xб + yв. Подставив координаты векторов, получим систему уравнений: -3 = 4x + 4y и 2 = -x - y. Решив эту систему уравнений, найдем x = 1 и y = -1. Таким образом, вектор а = 1б - в.
Что такое вектор?

Векторы могут быть использованы для описания движения в пространстве или на плоскости, а также для представления различных величин, таких как сила, скорость или ускорение.
Основными характеристиками вектора являются его направление и длина (или модуль). Направление указывает на то, куда направлен вектор, а длина показывает, насколько велик вектор. Вектор может быть представлен в виде координат или компонентов, которые указывают его положение на координатной оси.
Векторы могут быть складываться и вычитаться друг из друга, а также умножаться на скаляр – число. Эти операции называются сложением векторов, вычитанием векторов и умножением вектора на скаляр соответственно. Результатом сложения, вычитания и умножения будет новый вектор.
Примеры:
Вектор A = (2, 3) представляет собой вектор, который начинается в начале координат и заканчивается в точке с координатами (2, 3).
Вектор B = (4, -1) представляет собой вектор, который начинается в начале координат и заканчивается в точке с координатами (4, -1).
Вектор C = (1, 2, 3) представляет собой трехмерный вектор, который начинается в начале координат и заканчивается в точке с координатами (1, 2, 3).
Определение и основные характеристики вектора
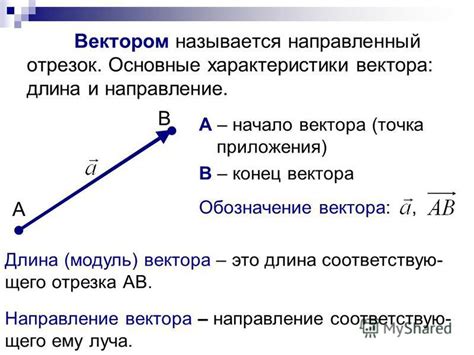
Основные характеристики вектора:
- Направление: вектор может быть направлен вдоль любой прямой в пространстве.
- Длина: длина вектора определяется его модулем или абсолютной величиной и обозначается символом.
- Точка приложения: каждый вектор начинается в определенной точке, называемой началом вектора.
Векторы могут быть представлены как геометрически, так и алгебраически. Геометрическое представление вектора – стрелка, которая иллюстрирует его направление и длину. Алгебраическое представление вектора – числовая запись, использующая координаты начала и конца вектора.
Например, вектор A может быть представлен алгебраически как A = (x1, y1), где x1 и y1 – координаты начала вектора, а emx2 и y2 – координаты конца вектора. Геометрически вектор A будет представлен стрелкой, которая показывает направление и длину вектора.
Свойства векторов
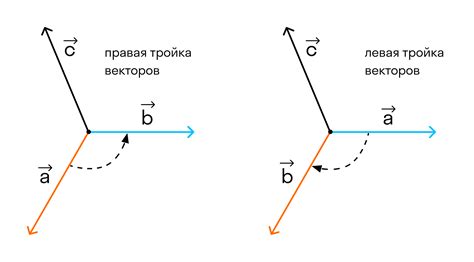
Векторы представляют собой математические объекты, которые имеют несколько важных свойств. Ниже приведены основные свойства векторов:
| Свойство | Описание |
|---|---|
| Длина | Длина вектора определяется как расстояние между началом и концом вектора. Она всегда больше или равна нулю. |
| Направление | Вектор имеет направление, которое определяется углом между направлением вектора и осью x в пространстве. Направление может быть положительным или отрицательным в зависимости от угла. |
| Сумма | Сумма двух векторов определяется путем сложения соответствующих компонент. Результатом сложения является новый вектор. |
| Скалярное произведение | Скалярное произведение двух векторов определяется как произведение длин векторов на косинус угла между ними. Результатом скалярного произведения является скалярная величина. |
Это основные свойства векторов, которые являются фундаментальными для понимания и использования векторной алгебры. Знание этих свойств позволяет более глубоко и точно работать с векторами в различных областях науки и техники.
Сложение векторов
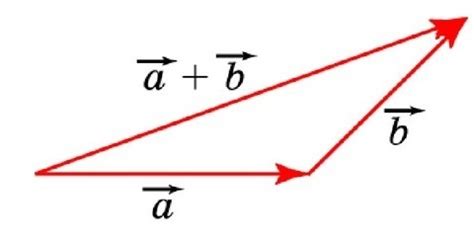
Закон параллелограмма гласит, что сумма двух векторов равна вектору, направление и длина которого определяются построением параллелограмма на основе этих двух векторов. То есть, чтобы сложить два вектора, нужно построить параллелограмм, сторонами которого будут эти векторы, а диагональю – искомый вектор.
Метод компонент основан на представлении векторов как суммы их компонент. Для сложения двух векторов по этому методу достаточно сложить их соответствующие компоненты. При этом, для двухмерных векторов, суммируются компоненты x и y, а для трехмерных векторов – x, y и z.
Пример:
Даны два вектора A и B:
A = (3, 2)
B = (1, -1)
Сложение двух векторов по методу компонент:
A + B = (3 + 1, 2 + (-1)) = (4, 1)
Сложение двух векторов по закону параллелограмма:
A + B = (3 + 1, 2 + (-1)) = (4, 1)
Выразить вектор через другие два
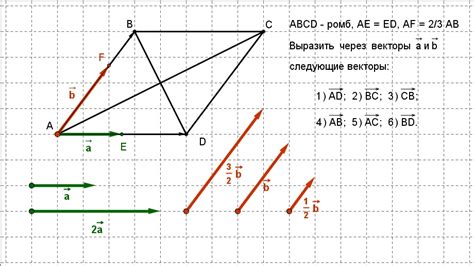
Для того чтобы выразить вектор через другие два, необходимо использовать операции линейной комбинации векторов.
Пусть даны два вектора a и b, а также требуемый вектор c. Чтобы найти координаты вектора c, необходимо решить систему линейных уравнений:
| c1 | = | a1 * x + b1 * y |
| c2 | = | a2 * x + b2 * y |
| c3 | = | a3 * x + b3 * y |
где x и y – неизвестные параметры, которые нужно найти.
Решив эту систему уравнений, мы найдем координаты вектора c, который будет выражен через векторы a и b.
Пример:
Даны векторы a = (1, 3, -2) и b = (2, -1, 4). Необходимо выразить вектор c через векторы a и b.
Решение:
Подставим координаты векторов в систему уравнений:
| c1 | = | a1 * x + b1 * y |
| c2 | = | a2 * x + b2 * y |
| c3 | = | a3 * x + b3 * y |
Получим систему уравнений:
| c1 | = | 1 * x + 2 * y |
| c2 | = | 3 * x + (-1) * y |
| c3 | = | (-2) * x + 4 * y |
Решим данную систему уравнений. Результатом будет:
c = (x + 2y, 3x - y, -2x + 4y)
Таким образом, вектор c выражен через векторы a и b следующим образом: c = (x + 2y, 3x - y, -2x + 4y).
Методы выражения вектора

Вектор может быть выражен через другие вектора при помощи различных методов. Рассмотрим несколько из них:
- Метод параллелограмма:
- Метод треугольника:
- Метод компонент:
Данный метод основан на идее построения параллелограмма на основе двух векторов. Если A и B - два вектора, то вектор C, являющийся диагональю построенного параллелограмма, можно выразить при помощи формулы C = A + B. Таким образом, вектор C выражается через векторы A и B.
Этот метод также основан на построении геометрической фигуры - треугольника. Если A и B - два вектора, а C - их сумма, то можно построить треугольник с вершинами в точках начала координат (0,0), A и B. Вектор С, являющийся диагональю этого треугольника, можно выразить при помощи формулы C = A - B. Таким образом, вектор C выражается через векторы A и B.
При использовании этого метода, вектор может быть выражен через его компоненты. Если вектор задан координатами (x, y), то его можно выразить как сумму двух векторов, A и B. Вектор A будет иметь координаты (x, 0), а вектор B - (0, y). Тогда исходный вектор C можно записать как C = A + B, где A и B выражены через координаты исходного вектора.
Каждый из этих методов позволяет выразить исходный вектор в зависимости от других векторов или его компонент. Понимание этих методов является важным для решения задач и работы с векторами в математике и физике.
Требования к исходным векторам
Для того чтобы выразить вектор через другие два, необходимо, чтобы все три вектора были линейно независимы. Линейная независимость означает, что ни один из векторов не может быть представлен в виде линейной комбинации других векторов. Если один из векторов может быть представлен в виде линейной комбинации других, то его нельзя выразить через остальные два.
Дополнительно, требуется, чтобы векторы желательно были ортогональными или, в идеале, ортонормированными. Векторы называются ортогональными, если их скалярное произведение равно нулю. Векторы называются ортонормированными, если они ортогональны и имеют длину (норму) равную единице.
Для наглядности и удобства часто используют таблицу, в которой указываются координаты исходных векторов и их свойства. Пример таблицы представлен ниже:
| Вектор | Координаты | Ортогональность | Ортонормированность |
|---|---|---|---|
| Вектор a | (a1, a2, a3) | нет | нет |
| Вектор b | (b1, b2, b3) | да | нет |
| Вектор c | (c1, c2, c3) | нет | да |
Из приведенной таблицы видно, что вектор b и c ортогональны, но не являются ортонормированными. Вектор a не ортогонален ни одному из остальных векторов и не является ортонормированным.
Примеры выражения вектора

Выразить вектор a через векторы b и c можно с использованием линейной комбинации:
| Пример | Выражение |
|---|---|
| Пример 1 | a = 2b + 3c |
| Пример 2 | a = -3b + 5c |
| Пример 3 | a = 0.5b - 1.2c |
В этих примерах коэффициенты перед векторами b и c определяются в зависимости от конкретной задачи или условий. Выражение вектора через другие два позволяет связать их и упростить решение задачи.
Пример 1: выражение вектора через два других
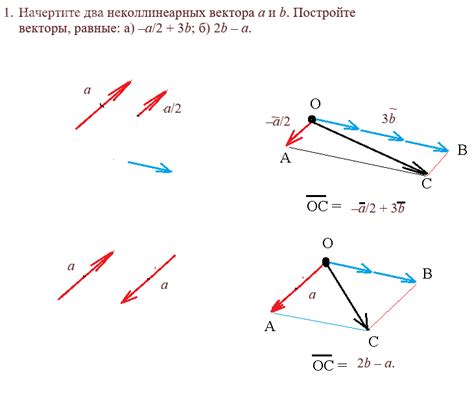
Предположим, что у нас есть два вектора A и B в двумерном пространстве. И мы хотим выразить третий вектор C через них.
Имеем:
| Вектор | Компоненты |
|---|---|
| A | a1, a2 |
| B | b1, b2 |
Выражение вектора C через A и B будет иметь вид:
| C | = x * A + y * B |
где x и y - коэффициенты, определяющие, какая часть вектора приходится на каждый из векторов A и B.
Например, если коэффициенты x = 2 и y = 3, то выражение будет выглядеть так:
| C | = 2 * A + 3 * B |
Таким образом, вектор C будет равен комбинации векторов A и B, где каждый компонент вектора C будет равен сумме соответствующих компонент векторов A и B, умноженных на соответствующие коэффициенты.




