В математике и физике векторы являются очень важными объектами. Они используются для описания различных физических величин, таких как скорость, сила, момент силы и т. д. Однако, векторы могут быть не только отдельными объектами, но и составлять особую группу, называемую взаимной тройкой. Взаимная тройка векторов представляет собой особую конфигурацию трех векторов, которая имеет определенные свойства и применения.
Для того чтобы три вектора образовали взаимную тройку, они должны удовлетворять двум основным условиям. Во-первых, они должны быть плоскими векторами, то есть лежать в одной плоскости. Во-вторых, сумма этих векторов должна равняться нулю. Это означает, что если мы сложим три вектора тройки, то получим нулевой вектор. Иными словами, каждый вектор из тройки можно выразить через два других вектора.
Взаимная тройка векторов имеет много применений в различных областях. Например, в физике она используется для описания силовых систем и равнодействующих сил. В геометрии она помогает в решении задач на нахождение площадей и объемов. Кроме того, взаимная тройка векторов является важным базисным инструментом в линейной алгебре и векторной алгебре.
Таким образом, взаимная тройка векторов представляет собой особую конфигурацию трех векторов, удовлетворяющих условиям плоскости и нулевой суммы. Она имеет широкое применение в различных областях и является важным инструментом в математике и физике.
Определение взаимной тройки векторов
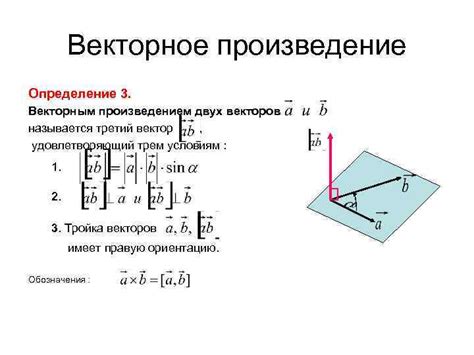
Таким образом, если имеется трехмерное пространство, то взаимная тройка векторов будет состоять из трех неколлинеарных векторов, таких что их геометрическая сумма равна нулю. Коллинеарность векторов означает, что они лежат на одной прямой и параллельны друг другу.
Взаимная тройка векторов можно представить графически в виде замкнутой фигуры, например, треугольника или параллелограмма. Такая фигура называется векторной диаграммой.
Взаимная тройка векторов играет важную роль в линейной алгебре и геометрии. Она позволяет решать различные задачи, связанные с векторами, такие как определение равновесия системы сил, вычисление площади треугольника и другие.
Свойства взаимной тройки векторов
1. Линейная зависимость
Взаимная тройка векторов называется линейно зависимой, если существуют такие коэффициенты, при которых их линейная комбинация равна нулевому вектору. В этом случае хотя бы один из векторов является линейной комбинацией двух других.
2. Линейная независимость
Если взаимная тройка векторов не является линейно зависимой, то она называется линейно независимой. Это означает, что векторы не могут быть выражены как линейные комбинации друг друга.
3. Ортогональность
Векторы взаимной тройки могут быть ортогональными, то есть перпендикулярными друг другу. Это означает, что угол между любыми двумя векторами равен 90 градусам.
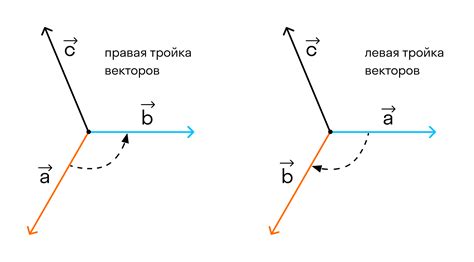
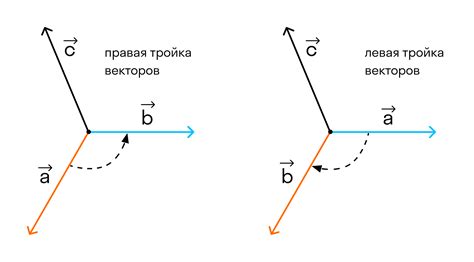
4. Правая и левая тройки векторов
Взаимная тройка векторов может быть либо правой, либо левой. Правая тройка обладает свойством, что направление векторного произведения первых двух векторов совпадает с направлением третьего вектора. Левая тройка – с противоположным направлением.
Эти свойства взаимной тройки векторов имеют не только теоретическое значение, но и находят широкое применение в различных областях науки и техники.
Расчет взаимной тройки векторов

Для определения взаимной тройки векторов необходимо проверить условия их линейной независимости. Пусть у нас есть три вектора A, B и C. Чтобы эти векторы были линейно независимы, необходимо, чтобы ни один из них не мог быть выражен через линейную комбинацию других двух векторов.
Для проверки линейной независимости векторов можно воспользоваться методом определителей. Для этого составим матрицу из координат векторов и вычислим ее определитель. Если определитель не равен нулю, то векторы являются линейно независимыми и образуют взаимную тройку.
Например, пусть у нас есть векторы:
| Вектор A | (1, 0, 0) |
| Вектор B | (0, 1, 0) |
| Вектор C | (0, 0, 1) |
Матрица из координат векторов:
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
Вычисляем определитель:
det = 1*(1*1-0*0)-0*(0*1-0*0)+0*(0*1-0*0) = 1
Так как определитель не равен нулю, векторы A, B и C являются линейно независимыми и образуют взаимную тройку векторов.
Геометрическое представление взаимной тройки векторов

Взаимная тройка векторов представляет собой группу трех векторов, которые связаны между собой определенными соотношениями. Геометрическое представление взаимной тройки векторов основано на понятиях направленных отрезков и пространственных углов.
Для геометрического представления взаимной тройки векторов используется специальная таблица, называемая таблицей направленных отрезков. В этой таблице каждый вектор представлен в виде направленного отрезка, начало которого соответствует началу системы координат, а конец - концу вектора.
| Вектор | Направление | Длина |
|---|---|---|
| Вектор AB | От начала координат до точки B | Длина AB |
| Вектор BC | От точки B до точки C | Длина BC |
| Вектор CA | От точки C до начала координат | Длина CA |
Геометрическое представление взаимной тройки векторов позволяет визуально представить их в пространстве и оперировать понятиями направления и длины каждого вектора. Это полезно при решении задач, связанных с геометрией и физикой.
Применение взаимной тройки векторов в математике

Первое применение взаимной тройки векторов - это решение систем линейных уравнений. При помощи метода Крамера можно найти значения неизвестных, используя взаимную тройку векторов. Этот метод особенно удобен, когда система имеет трехмерное представление.
Взаимная тройка векторов также используется при решении задач о векторном произведении. Это позволяет определить площадь треугольника, образованного этими векторами. Зная величину взаимного произведения, можно определить и направление поворота треугольника.
Другое важное применение взаимной тройки векторов - это определение взаимно перпендикулярных векторов. При помощи ортогонализации векторов можно построить базис в пространстве. Это особенно полезно при решении задач линейной алгебры и геометрии в трехмерном пространстве.
Таким образом, использование взаимной тройки векторов в математике позволяет решать различные задачи, связанные с линейной алгеброй, геометрией и системами уравнений. Она является важным инструментом для анализа и решения математических проблем, особенно в трехмерном пространстве.
Применение взаимной тройки векторов в физике
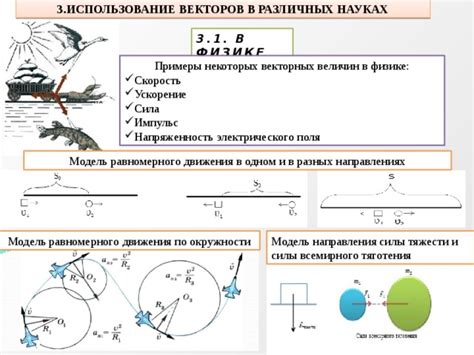
Взаимная тройка векторов широко применяется в физике для описания момента силы и угла между векторами. Момент силы представляет собой векторную величину, которая характеризует вращательное действие силы относительно заданной точки.
Для определения момента силы необходимо задать точку отсчета и определить векторное произведение силы на вектор, соединяющий точку отсчета и точку приложения силы. Взаимная тройка векторов позволяет определить направление и величину момента силы.
Также взаимная тройка векторов используется для определения угла между векторами. Угол между двумя векторами можно найти с помощью взаимной тройки, в которой одним из векторов является векторное произведение исходных векторов.
Применение взаимной тройки векторов в физике позволяет более точно и наглядно описывать вращательные явления, а также находить углы между векторами. Это значительно облегчает работу с векторными величинами в физических задачах и помогает лучше понять законы вращательного движения и взаимодействия сил.
Применение взаимной тройки векторов в графике
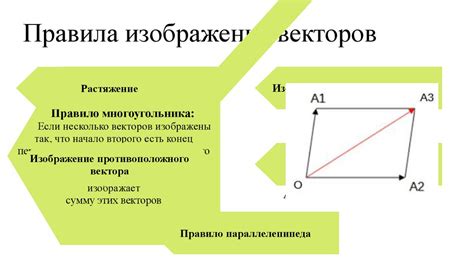
Взаимная тройка векторов, также известная под названием трехмерный базис, играет важную роль в графике. Векторы в этой тройке образуют оси координат X, Y и Z, которые используются для определения положения и ориентации объектов в трехмерном пространстве.
Работа с взаимной тройкой векторов позволяет создавать сложные трехмерные модели, реалистичные анимации и эффекты в графике. Векторы могут задавать координаты вершин объектов, направления источников света, смещение и вращение камеры, а также другие параметры, влияющие на визуализацию сцены.
Каждый вектор в тройке представляет собой направление и длину. Они могут быть заданы в виде числовых значений или символов, в зависимости от используемой графической библиотеки или программы. Векторы могут быть также нормализованы, то есть приведены к единичной длине, чтобы удобнее работать с ними и производить математические операции.
Применение взаимной тройки векторов в графике позволяет реализовать различные эффекты, такие как отражение и преломление света, смещение искажений, создание теней и множество других визуальных эффектов. При использовании векторов правильно можно добиться реалистичности и глубины изображений.
Взаимная тройка векторов играет важную роль в графике и позволяет реализовывать сложные трехмерные сцены и эффекты. Она является основой для работы с трехмерной графикой и способствует созданию реалистичных и выразительных изображений.
Примеры использования взаимной тройки векторов
- В физике применяются взаимные тройки векторов для описания сил, действующих на тело. Например, тройку сил можно использовать для определения равновесия тела или движения под действием нескольких сил.
- В геометрии взаимные тройки векторов используются для определения плоскостей в пространстве. Такие тройки могут быть использованы для нахождения точек пересечения плоскостей или для определения положения точки относительно плоскости.
- В компьютерной графике взаимные тройки векторов используются для определения осей координат и системы координат в трехмерном пространстве. Такие тройки могут быть использованы для определения положения и ориентации 3D-объектов.
- В механике взаимные тройки векторов используются для описания вращательного движения. Такие тройки могут быть использованы для определения моментов сил и осей вращения.
Это лишь некоторые примеры применения взаимной тройки векторов в различных областях. В общем, взаимная тройка векторов позволяет учитывать не только значение вектора, но и его направление и ориентацию. Это делает ее мощным инструментом для анализа и решения различных задач.




