Треугольник – это геометрическая фигура, которая состоит из трех сторон и трех углов. Важно отметить, что существуют различные типы треугольников, каждый из которых обладает своими уникальными свойствами. Для понимания и изучения треугольников необходимо знать их основные характеристики и особенности.
Одной из важных характеристик треугольника является взаимная перпендикулярность его сторон. Взаимно перпендикулярные стороны треугольника – это такие стороны, которые перпендикулярны друг другу. Другими словами, они образуют прямой угол в точке их пересечения.
Свойство взаимно перпендикулярных сторон треугольника позволяет нам делать определенные выводы о его углах и других свойствах. В частности, если две стороны треугольника перпендикулярны друг другу, то третья сторона является гипотенузой прямоугольного треугольника. Кроме того, из данного свойства следует, что один из углов треугольника является прямым углом.
Взаимно перпендикулярные стороны треугольника также имеют важное геометрическое значение. Они являются основой для решения множества задач и построения разнообразных фигур.
Понимание и использование свойств взаимно перпендикулярных сторон треугольника позволяет выполнять различные геометрические вычисления и конструировать разнообразные фигуры с точностью и эффективностью. Изучение данного свойства и его применение позволяет решать задачи, связанные с построением и анализом треугольников, и расширяет наши знания и навыки в области геометрии.
Определение взаимно перпендикулярных сторон треугольника
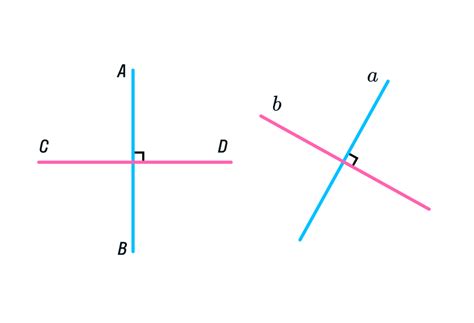
Для треугольника ABC взаимно перпендикулярные стороны могут быть обозначены следующим образом: AB и BC, BC и CA, или CA и AB.
Свойства взаимно перпендикулярных сторон треугольника:
- Взаимно перпендикулярные стороны равны по длине.
- Треугольник, у которого две стороны взаимно перпендикулярны, является прямоугольным.
- Перпендикуляр, проведенный из вершины треугольника к противоположной стороне, делит эту сторону на две равные части.
- Взаимно перпендикулярные стороны, вместе с отрезком, соединяющим две вершины, образуют прямоугольный треугольник.
Знание о взаимно перпендикулярных сторонах треугольника помогает в решении задач по геометрии и позволяет определить некоторые свойства и отношения внутри треугольника.
Определение понятия

Каждый треугольник имеет три стороны, и в некоторых случаях две из них могут быть перпендикулярными. В таких треугольниках обычно выделяют особый вариант, называемый прямоугольным треугольником.
В прямоугольном треугольнике взаимно перпендикулярные стороны являются катетами, а третья сторона, не перпендикулярная ним, является гипотенузой. Гипотенуза соответствует греческой букве "γ" (гамма), а катеты - "α" (альфа) и "β" (бета).
Взаимно перпендикулярные стороны треугольника играют важную роль в различных геометрических конструкциях и задачах. Они могут использоваться для определения геометрических фигур и расчета их свойств.
| Стороны треугольника | Определяемое понятие |
|---|---|
| Два катета | Прямоугольный треугольник |
| Гипотенуза и один катет | Определение косинуса угла |
| Гипотенуза и другой катет | Определение синуса или косинуса угла |
Изучение взаимно перпендикулярных сторон треугольника предоставляет возможность решать сложные геометрические задачи и строить простые и элегантные геометрические построения.
Условия существования взаимно перпендикулярных сторон

Для того чтобы треугольник имел взаимно перпендикулярные стороны, необходимо выполнение следующих условий:
- Треугольник должен быть прямоугольным.
- В прямоугольном треугольнике сторона, противолежащая прямому углу, должна быть гипотенузой.
- Другие две стороны треугольника, противолежащие острым углам, должны быть взаимно перпендикулярными.
Эти условия являются не только необходимыми, но и достаточными для того, чтобы треугольник имел взаимно перпендикулярные стороны.
Примеры треугольников с взаимно перпендикулярными сторонами

Вот некоторые примеры треугольников с взаимно перпендикулярными сторонами:
- Прямоугольный треугольник: одна из сторон является основанием треугольника, а две другие стороны являются катетами, перпендикулярными основанию.
- Равнобедренный прямоугольный треугольник: две стороны являются катетами, перпендикулярными основанию, и одна сторона является гипотенузой.
- Остроугольный треугольник: стороны, проведенные из вершин с острыми углами, могут быть перпендикулярными друг другу.
Треугольники с взаимно перпендикулярными сторонами имеют свои особенности и свойства, которые могут быть использованы в различных математических задачах и конструкциях.
Зависимость между величиной угла и длиной стороны
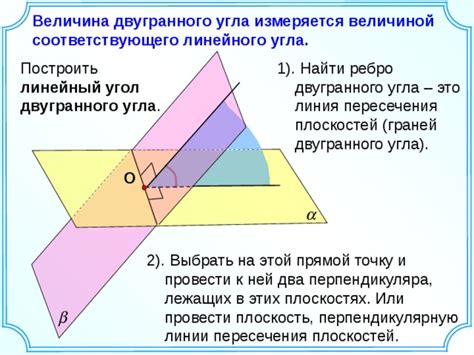
Угол и сторона треугольника взаимно связаны. Изменение величины угла треугольника может привести к изменению длины стороны, а изменение длины стороны может оказать влияние на величину угла.
В треугольнике с прямым углом (90 градусов) длина гипотенузы зависит от длин катетов и может быть найдена с помощью теоремы Пифагора. Это свойство позволяет нам использовать прямоугольные треугольники в решении задач по нахождению длин сторон или углов.
Величина угла также может быть использована для нахождения площади треугольника. Формула для вычисления площади треугольника имеет вид:
Площадь = 0,5 * сторона * сторона * sin(угол)
Из этой формулы видно, что при увеличении величины угла площадь треугольника также увеличивается.
Кроме того, величина стороны может влиять на величину угла. Например, в треугольнике с двумя равными сторонами (равнобедренный треугольник), углы, противолежащие равным сторонам, также равны. А в прямоугольном треугольнике длина гипотенузы зависит от длин двух катетов, и изменение длины сторон треугольника приведет к изменению величины углов треугольника.
Таким образом, между величиной угла и длиной стороны треугольника существует взаимосвязь, которую можно использовать для решения задач, связанных с треугольниками и их свойствами.
Особенности применения взаимно перпендикулярных сторон в математике

Прежде всего, взаимно перпендикулярные стороны треугольника позволяют определить его высоты. Высота – это отрезок, проведенный из вершины треугольника к противоположной стороне и перпендикулярный ей. Взаимно перпендикулярные стороны являются основными сторонами для построения высоты, что делает их важными инструментами для изучения треугольников.
Кроме того, взаимно перпендикулярные стороны треугольника помогают определить основания биссектрис. Биссектриса – это прямая, делящая угол треугольника пополам. Взаимно перпендикулярные стороны могут быть использованы для построения основания биссектрисы, что позволяет нам рассматривать углы треугольника с точки зрения их деления и находить важные характеристики этих углов.
Кроме того, взаимно перпендикулярные стороны также позволяют определить центр окружности, вписанной в треугольник. Окружность вписана в треугольник, если она касается всех его сторон. Взаимно перпендикулярные стороны позволяют нам определить точку, из которой будут проведены касательные линии к сторонам треугольника, что позволяет найти центр окружности и изучать свойства треугольника в зависимости от этой окружности.
Таким образом, взаимно перпендикулярные стороны треугольника играют важную роль в математике и позволяют проводить разнообразные исследования и вычисления, связанные с треугольниками и их характеристиками. Изучение этих свойств помогает нам лучше понять и описать геометрию треугольников и использовать эту информацию в решении различных задач.
Геометрическое приложение взаимно перпендикулярных сторон

Использование этого свойства в геометрии позволяет решать различные задачи. Например, если известна длина одной из взаимно перпендикулярных сторон треугольника, то можно определить длины остальных сторон с помощью теоремы Пифагора. Это чрезвычайно полезное знание при решении множества задач, связанных с расчетами в треугольниках.
Геометрическое приложение взаимно перпендикулярных сторон также проявляется при решении задач на нахождение площади треугольника. Если известны длины взаимно перпендикулярных сторон треугольника, то можно использовать формулу для расчета площади прямоугольника: площадь равна произведению длин перпендикулярных сторон. Такое применение свойства позволяет упростить расчеты и решить задачу более эффективно.
Взаимно перпендикулярные стороны треугольника также находят свое применение в построении различных фигур. Например, они позволяют построить прямоугольник, если известны длины двух его сторон. Также с помощью взаимно перпендикулярных сторон можно построить прямоугольный треугольник, зная длину одной его стороны и одну из его остроугольных вершин. Такие приложения помогают в различных задачах, включая архитектуру, строительство и геодезию.
Таким образом, знание и использование свойств взаимно перпендикулярных сторон треугольника имеет большое практическое значение и является важным элементом геометрических расчетов и построений.
Теорема, связывающая взаимно перпендикулярные стороны и углы треугольника
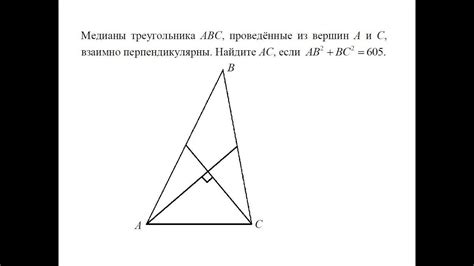
Теорема: В треугольнике взаимно перпендикулярными являются три пары сторон и углов:
- Перпендикулярные стороны образуют прямой угол.
- Углы, прилежащие к перпендикулярным сторонам, являются смежными.
- Сумма углов, прилежащих к перпендикулярным сторонам, равна 180 градусов.
То есть, если две стороны треугольника взаимно перпендикулярны, то они образуют прямой угол, а углы, прилежащие к этим сторонам, будут смежными и их сумма будет равна 180 градусов.
Такая теорема является важным инструментом в геометрии и находит свое применение при решении различных задач, связанных с треугольниками.
Практическое применение взаимно перпендикулярных сторон в архитектуре и конструкциях

Одно из практических применений взаимно перпендикулярных сторон состоит в определении квадратности и прямоугольности строительных объектов. Например, для построения прямоугольников и параллелограммов используются перпендикулярные стороны, что позволяет создавать геометрически правильные и симметричные формы.
Другим примером практического применения является строительство ограждений и заборов. Когда строительные элементы, такие как столбы и панели, располагаются взаимно перпендикулярно, это придает ограде прочность и устойчивость. Кроме того, использование перпендикулярных сторон может создавать эффект открытости и простора.
Также взаимно перпендикулярные стороны могут быть использованы в архитектурных элементах, таких как окна и двери. При расположении окон и дверей в плоскостях, пересекающихся под прямым углом, достигается более эргономичное размещение элементов и улучшается освещение внутренних помещений.
Кроме того, перпендикулярные стороны могут быть использованы для создания композиционных решений в дизайне интерьеров. Например, расположение мебели и предметов интерьера взаимно перпендикулярно может создать гармоничный баланс и ощущение упорядоченности в помещении.
Таким образом, взаимно перпендикулярные стороны треугольника находят широкое применение в архитектуре и конструкциях, позволяя достигать прочности, стабильности и эстетической привлекательности. Они играют важную роль в создании функциональных и эргономичных строений, а также придают комфорт и гармонию в дизайне помещений.




