Эксцесс — это одна из важных статистических характеристик распределения вероятностей. Он позволяет определить, насколько форма распределения отличается от нормального распределения. Когда эксцесс меньше нуля, это означает, что распределение имеет «плоскую» форму. В статистике эксцесс широко используется для анализа данных и оценки их округленности.
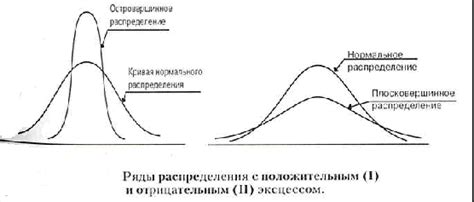
Возможные значения эксцесса для нормального распределения составляют 0. Если эксцесс больше нуля, это означает, что распределение имеет «островершинную» форму и более вытянутое на концах. Если же эксцесс меньше нуля, это указывает на наличие «плоской» формы распределения и более тяжелые хвосты. Значение эксцесса позволяет провести сравнение между различными распределениями и выявить их особенности.
Например, если эксцесс меньше нуля для некоторой выборки, это говорит о том, что данные имеют плоскую форму, а значит, значения сконцентрированы около среднего значения. Кроме того, такое распределение будет иметь тяжелые хвосты, что означает, что вероятность появления значительно больших или маленьких значений будет выше, чем для нормального распределения.
Интерпретация эксцесса меньше нуля может быть полезной при анализе данных и принятии решений. Например, если исследуемая выборка имеет плоскую форму и тяжелые хвосты, это может указывать на наличие выбросов или аномалий в данных. Также эксцесс может использоваться для определения наилучшего приближения распределения и прогнозирования будущих значений. Понимание и интерпретация эксцесса меньше нуля позволяет получить дополнительную информацию о данных и эффективно использовать ее в анализе.
Эксцесс меньше нуля

Если эксцесс меньше нуля, это означает, что в распределении случайной величины присутствует "сглаженная" или "плоская" форма. В таком распределении значения случайной величины будут более равномерно распределены и иметь меньшую концентрацию около среднего значения.
Когда эксцесс меньше нуля, график распределения будет иметь более широкую или "плоскую" форму. Это может указывать на то, что данные имеют менее ярко выраженную скошенность и более равномерное распределение значений. В таком случае, мы можем ожидать, что вероятность встретить значения, находящиеся дальше от среднего значения, будет меньше.
Однако, не стоит сразу делать вывод о характере распределения данных только по значению эксцесса. Для полного анализа стоит учитывать и другие статистические показатели, такие как среднее значение, медиана и разброс данных.
| Значение эксцесса | Тип распределения | Описание |
|---|---|---|
| Меньше нуля (<0) | Плоское распределение | Значения равномерно распределены вокруг среднего |
| Равно нулю (=0) | Нормальное распределение | Значения сосредоточены вокруг среднего симметрично |
| Больше нуля (>0) | Острое распределение | Значения сосредоточены ближе к среднему |
Изучение эксцесса и других статистических показателей помогает лучше понять форму и характер распределения данных. Это важно для последующих статистических исследований и принятия соответствующих решений на основе этих данных.
Понятие эксцесса в статистике
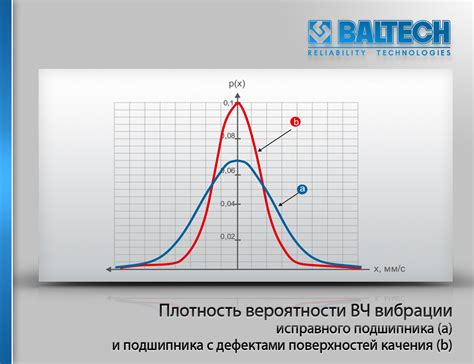
Эксцесс больше нуля означает, что пик распределения более острый и более высокий, чем у нормального распределения. То есть, вероятность нахождения значений ближе к среднему значению выше, чем вероятность нахождения значений в хвостах распределения.
В случае, когда эксцесс меньше нуля, распределение имеет широкий и низкий пик. Это означает, что вероятность нахождения значений ближе к среднему значению ниже, чем вероятность нахождения значений в хвостах распределения.
Таким образом, эксцесс позволяет нам получить дополнительную информацию о форме и остроте распределения данных. Он является важным инструментом для анализа данных и принятия решений на основе их распределения.
Значение эксцесса меньше нуля
Значение эксцесса может быть положительным, нулевым или отрицательным. Значение эксцесса меньше нуля указывает на то, что форма распределения имеет "плоские хвосты". Более конкретно, это означает, что данные имеют большее количество выбросов (значений, которые сильно отклоняются от среднего) в хвостах распределения по сравнению с нормальным распределением.
Когда значение эксцесса меньше нуля, это может указывать на наличие у данных сильного отклонения от нормальности. Такие данные могут быть устроены, например, таким образом, что имеются ярко выраженные "выбросы" с большими значениями в хвостах распределения. Это необходимо учитывать при анализе данных и выборе соответствующих методов статистического анализа.
Влияние эксцесса на форму распределения
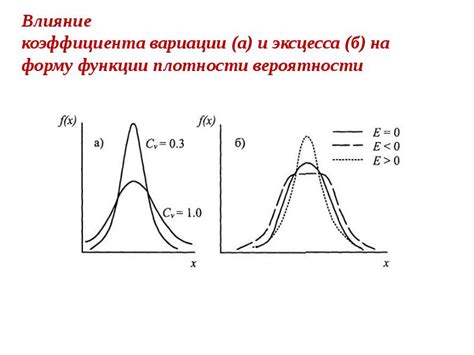
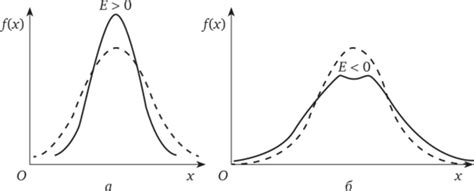
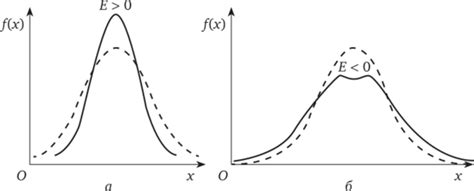
Влияние эксцесса на форму распределения можно проиллюстрировать на примере графиков. Рассмотрим два распределения: одно с нормальным эксцессом (равным нулю) и другое с отрицательным эксцессом (меньше нуля).
- Нормальное распределение: при нулевом эксцессе (кривая ЗВО) хвосты распределения симметрично уходят в бесконечность. Такое распределение имеет стандартную колоколообразную форму. Хвосты нормального распределения несут одинаковую вероятность появления экстремальных значений в обе стороны.
- Распределение с отрицательным эксцессом (плоское распределение): хвосты здесь более плоские, или «легкие». Высокие значения встречаются реже, чем при нормальном распределении. Вероятность появления экстремальных значений снижается. Распределение с отрицательным эксцессом сильно отличается от нормального и характеризуется широким разбросом значений.
Таким образом, эксцесс оказывает влияние на форму распределения и позволяет сделать выводы о его свойствах. Распределения с отрицательным эксцессом, как правило, имеют легкие хвосты и больший разброс значений. Это может быть полезным для анализа данных, когда необходимо выделить экстремальные значения и выявить необычные явления.
Распределение с отрицательным эксцессом
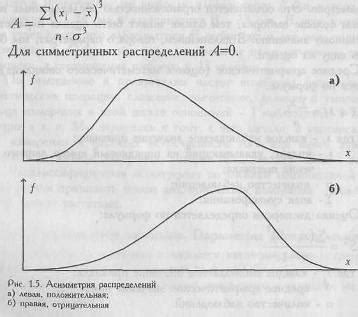
Распределение с отрицательным эксцессом может означать, что данные имеют более равномерное распределение по сравнению с нормальным. Оно не имеет ярко выраженных пиков или тяжелых хвостов, а сконцентрировано вокруг среднего значения. Такие данные можно назвать более "расплывчатыми" или менее "сгруппированными".
На практике, распределения с отрицательным эксцессом встречаются в различных областях, например в экономике, где они могут указывать на более плавное или стабильное поведение переменных.
Интерпретация эксцесса данных с отрицательным значением всегда требует анализа конкретного контекста и области применения. Важно учитывать, что эксцесс - это один из многих параметров описания данных, и его значение всегда следует рассматривать в контексте других характеристик распределения.
Отличие от распределений с положительным и нулевым эксцессом
Распределения с положительным эксцессом, также известные как "тяжелые хвосты", обладают более крутыми и вытянутыми хвостами. Это означает, что вероятность появления значения, находящегося далеко от среднего, выше, чем в распределении с нулевым или отрицательным эксцессом.
Распределения с нулевым эксцессом, также называемые "нормальными" распределениями, имеют более симметричную форму. Они отличаются тем, что вероятность появления значения вблизи среднего значения выше, чем вблизи хвостов или экстремальных значений.
Распределения с отрицательным эксцессом, известные как "легкие хвосты", имеют более плоскую форму и менее вытянутые хвосты, чем распределения с положительным эксцессом. Вероятность появления значения далеко от среднего значительно ниже, чем в распределениях с положительным эксцессом.
Таким образом, значение эксцесса позволяет сделать вывод о форме распределения случайной величины и о хвостах распределения.
Возможные причины отрицательного эксцесса

Вероятность отрицательного эксцесса возникает по следующим причинам:
| Причина | Описание |
|---|---|
| 1. Левосторонняя асимметрия | Если выборка имеет длинный хвост слева, значения находятся ближе к нулю, что приводит к отрицательному эксцессу. |
| 2. Небольшой размер выборки | Маленький размер выборки может приводить к случайным флуктуациям, которые могут негативно влиять на эксцесс и приводить к его отрицательному значению. |
| 3. Аномальные значения | Наличие выбросов или аномально высоких/низких значений может искажать форму распределения и приводить к отрицательному эксцессу. |
Важно учитывать, что отрицательный эксцесс сам по себе не указывает на проблему или ошибку данных. Он просто предоставляет информацию о форме распределения значений в выборке. Интерпретация отрицательного эксцесса требует дополнительного анализа контекста и других статистических мер.
Как интерпретировать отрицательный эксцесс
Отрицательный эксцесс указывает на то, что значения в выборке имеют более тонкое или отрицательное хвостовое распределение, чем у нормального распределения. Это означает, что выборка имеет больше экстремальных значений с низкой вероятностью и меньше значений вокруг центральной части распределения.
Если эксцесс меньше нуля, это может указывать на то, что выборка имеет более "плоский" или "удлиненный" вид, чем ожидалось. То есть, значения в выборке могут иметь больше разброса и быть более "распределены по хвостам" в сравнении с нормальным распределением.
Отрицательный эксцесс может быть интерпретирован как сигнал о наличии экстремальных значений или выбросов в данных. Это может указывать на то, что в выборке есть значения, которые сильно отличаются от остальных и могут существенно влиять на результаты анализа.
При интерпретации отрицательного эксцесса важно также учитывать контекст и предметную область исследования, а также проводить дополнительные статистические тесты или анализы для подтверждения выводов. Для более точной интерпретации эксцесса можно также использовать другие меры распределения, такие как асимметрия или коэффициент вариации.
Примеры распределений с отрицательным эксцессом
Отрицательный эксцесс означает, что значения случайной величины в выборке имеют более плоское распределение, чем нормальное распределение.
Ниже приведены примеры некоторых распределений с отрицательным эксцессом:
| Название | Описание | Пример |
|---|---|---|
| Равномерное распределение | Все значения равновероятны |  |
| Распределение Лапласа | Симметричное распределение вокруг среднего значения |  |
| Распределение Хи-квадрат | Распределение суммы квадратов независимых стандартных нормальных переменных |  |
Эти примеры иллюстрируют различные типы распределений с отрицательным эксцессом, которые могут возникать в статистическом анализе данных. Понимание этих распределений позволяет более точно интерпретировать полученные результаты.




