Неравенства являются важной частью математики и используются для описания сравнения двух чисел или выражений. Знание того, как найти решение неравенства, позволяет нам находить значения переменных, которые удовлетворяют определенным условиям.
В случае неравенства, находим решение, соответствующее наибольшему значению. Это означает, что ищем наибольшую возможную величину, которую может принимать переменная при выполнении условия неравенства.
Например, рассмотрим неравенство x + 2 > 5. Чтобы найти наибольшее решение, необходимо найти наибольшее значение переменной x, при котором неравенство будет выполняться.
Для этого мы изначально имеем неравенство x + 2 > 5. Применим операцию вычитания 2 с обеих сторон неравенства и получим x > 3. Таким образом, наибольшее решение данного неравенства будет x = 3, так как любое значение x больше 3 также удовлетворяет условию.
Важно помнить, что при решении неравенства может быть множество значений, удовлетворяющих условию. Таким образом, наибольшее решение указывает на максимальное значение переменной, при котором неравенство будет верным.
Методы нахождения наибольшего решения неравенства
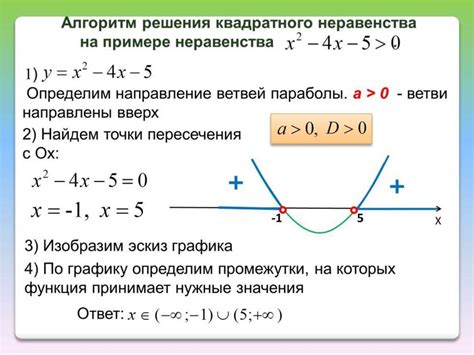
Для нахождения наибольшего решения неравенства можно применять различные методы. Ниже представлены несколько из них:
- Использование графического метода. Для этого нужно построить график функции, заданной в неравенстве, и найти точку на графике, где функция достигает максимального значения. Эта точка будет являться наибольшим решением неравенства.
- Использование метода подстановки. Для этого нужно подставить в неравенство различные значения переменных, начиная с наибольшего, и проверять, выполняется ли неравенство для каждого значения. Найти последнее значение, при котором неравенство выполняется, и оно будет являться наибольшим решением.
- Использование метода производных. Если функция, заданная в неравенстве, имеет производную, то можно найти критические точки функции, равномерно распределенные на интервале, и проверить знак производной в этих точках. Если производная положительна слева от критической точки и отрицательна справа, то эта точка будет являться максимумом функции и, следовательно, наибольшим решением неравенства.
Важно помнить, что каждый метод имеет свои ограничения и может быть применен только в определенных случаях. Также стоит отметить, что для некоторых неравенств наибольшего решения может не существовать.
Каким образом нахождение наибольшего решения влияет на задачи

Нахождение наибольшего решения неравенства играет важную роль во многих задачах. Знание наибольшего значения переменной помогает определить максимальные возможности или ограничения, которые могут быть применены в контексте конкретной проблемы или ситуации.
- Оптимизация: Задачи оптимизации часто требуют нахождения наибольшего значения функции при определенных ограничениях. Например, в задаче максимизации прибыли на предприятии, нахождение наибольшего решения может помочь определить оптимальное количество производимого товара.
- Планирование ресурсов: В различных отраслях экономики и бизнеса, нахождение наибольшего значения переменной может быть полезным для определения оптимального использования ресурсов, таких как рабочая сила, материалы или финансы.
- Ограничения проекта: В проектном менеджменте, нахождение наибольшего решения может помочь определить максимальное количество проектных задач, которые могут быть выполнены в ограниченный срок или с ограниченными ресурсами.
- Математические модели: В науке и инженерии, нахождение наибольшего значения может быть важным для определения оптимальных параметров в математических моделях, которые описывают физические или биологические системы.
Таким образом, нахождение наибольшего решения неравенства является ключевым шагом в решении множества задач, где требуется определить оптимальное значение переменной в заданном контексте.
Значение нахождения наибольшего решения неравенства в математике
В математике нахождение наибольшего решения неравенства имеет большое значение, так как позволяет определить максимальное значение переменной, при котором выполнение неравенства остается истинным.
Решение неравенства состоит из всех значений переменной, при которых неравенство выполняется. Найдя наибольшее решение неравенства, мы можем установить верхнюю границу для значения переменной, которая не нарушит условия неравенства.
Нахождение наибольшего решения неравенства может быть полезным в различных прикладных задачах. Например, при оптимизации процессов или ресурсов, можно использовать результаты математических моделей с ограничениями, заданными неравенствами. Нахождение наибольшего решения позволяет определить максимальное использование ресурсов при соблюдении данных ограничений.
Визуализация наибольшего решения неравенства может быть представлена в виде графика или таблицы. Для удобства, можно использовать таблицу, где будут представлены значения переменной и соответствующие значения неравенства при данных значениях. Таким образом, можно наглядно увидеть, при каких значениях переменной неравенство будет выполняться, а при каких - нет.
| Значение переменной | Значение неравенства |
|---|---|
| 1 | 8 > 5 |
| 2 | 10 > 5 |
| 3 | 12 > 5 |
| 4 | 14 > 5 |
В приведенном примере таблицы, наибольшее решение неравенства будет равно 4, так как при значениях переменной 5 и больше неравенство перестает выполняться. Таким образом, 4 будет максимальным допустимым значением переменной при выполнении данного неравенства.
Примеры нахождения наибольшего решения неравенства
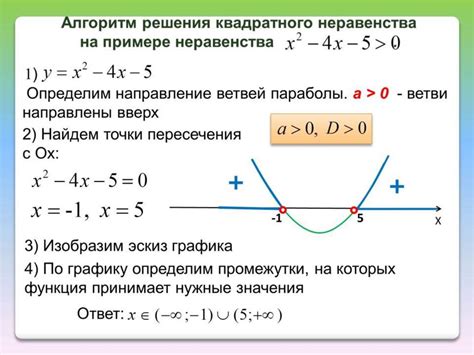
Для нахождения наибольшего решения неравенства необходимо использовать методы алгебры и графики. Рассмотрим несколько примеров.
Пример 1:
Решим неравенство 2x + 3 > 5.
Вычитаем 3 из обеих частей неравенства: 2x > 2.
Делим обе части неравенства на 2: x > 1.
Таким образом, наибольшим решением данного неравенства является x > 1.
Пример 2:
Решим неравенство x^2 - 4x + 3 < 0.
Факторизуем левую часть неравенства: (x - 1)(x - 3) < 0.
Определим знаки множителей: (x - 1) < 0 и (x - 3) < 0.
Решим первое неравенство: x - 1 < 0. Добавляем 1 ко всем частям: x < 1.
Решим второе неравенство: x - 3 < 0. Добавляем 3 ко всем частям: x < 3.
Таким образом, наибольшим решением данного неравенства является x < 1.
Пример 3:
Решим неравенство |2x - 5| > 3.
Разбиваем неравенство на два случая:
| Случай 1: | Случай 2: |
|---|---|
| 2x - 5 > 3 | 2x - 5 < -3 |
| Вычитаем 5 из обеих частей неравенства: 2x > 8 | Вычитаем 5 из обеих частей неравенства: 2x < 2 |
| Делим обе части неравенства на 2: x > 4 | Делим обе части неравенства на 2: x < 1 |
Таким образом, наибольшим решением данного неравенства является x > 4.
Практическое применение нахождения наибольшего решения неравенства

Оптимизация процессов:
В экономике и менеджменте нахождение наибольшего решения неравенства позволяет оптимизировать различные процессы. Например, при оптимизации производства можно найти наибольшее количество продукции, которую можно произвести при заданных условиях, таких как ограничения по ресурсам или бюджету.
Определение максимального значения функции:
В математике и физике нахождение наибольшего решения неравенства позволяет определить максимальное значение функции. Например, при решении задачи о максимизации прибыли или минимизации затрат, нахождение наибольшего решения помогает определить оптимальные значения переменных для достижения желаемых результатов.
Определение границ и ограничений:
В различных научных и инженерных областях нахождение наибольшего решения неравенства позволяет определить границы и ограничения для различных параметров. Например, в строительстве можно определить максимальную нагрузку, которую может выдержать конструкция, или максимальное значение напряжения, которое не приведет к разрушению материала.
Решение задач оптимального распределения ресурсов:
В задачах оптимального распределения ресурсов, таких как расчет оптимального плана производства или оптимального расписания задач, нахождение наибольшего решения неравенства играет ключевую роль. Наибольшее значение переменной в данном случае представляет оптимальное использование ресурсов для достижения поставленных целей.
Правила и условия для нахождения наибольшего решения неравенства
При решении неравенств существуют определенные правила и условия для нахождения наибольшего решения. Вот некоторые из них:
- Первым шагом необходимо привести неравенство к более простому виду, например, выразить переменную на одной стороне, а числа на другой.
- Если имеется деление на переменную, необходимо учесть знак переменной. Если переменная положительная, то при умножении/делении на положительное число знак неравенства не меняется, а при умножении/делении на отрицательное число знак меняется на противоположный.
- Если в неравенстве имеется умножение/деление на отрицательное число, то знак неравенства также меняется на противоположный.
- Если в неравенстве присутствуют скобки, необходимо раскрыть их и упростить выражение.
- В неравенстве могут присутствовать различные математические операции, такие как сложение, вычитание, умножение и деление. Необходимо последовательно применять эти операции для упрощения выражения.
- При выполнении операций с неравенствами необходимо учитывать порядок выполнения операций, а именно сначала выполнять умножение и деление, а затем сложение и вычитание.
- Если все переменные сократились, остается неравенство с числовым выражением. Оно может быть решено с помощью обычных правил сравнения чисел.
- Полученное решение неравенства может быть проверено подстановкой в исходное неравенство. Если полученное значение удовлетворяет неравенству, то оно является допустимым решением.
Правильное применение этих правил и условий позволяет найти наибольшее решение неравенства, которое удовлетворяет заданным условиям и ограничениям.




