Угол между диагоналями прямоугольника – это угол, который образуется между линиями, соединяющими противоположные углы. Этот угол является одним из ключевых параметров прямоугольника и может быть расчитан исходя из длин диагоналей.
Для расчёта угла между диагоналями прямоугольника можно использовать геометрическую формулу. Для начала, необходимо найти значения длин диагоналей pr и qr. Затем, используя формулу, вычислить угол a:
a = atan(pr / qr)
Где atan – это арктангенс, pr – длина первой диагонали, qr – длина второй диагонали. Полученное значение угла a будет задано в радианах.
Чтобы перевести угол a из радианов в градусы, можно воспользоваться формулой:
Угол в градусах = a * (180 / π)
Где π – это значение числа Пи, примерно равное 3.14159.
Рассмотрим пример. Пусть у нас есть прямоугольник с диагоналями длиной pr = 4 и qr = 3. Используя формулу, найдём угол a:
a = atan(4 / 3) ≈ 0.93 радиан
Приближённо, угол между диагоналями прямоугольника будет составлять примерно 0.93 радиан или около 53 градусов.
Что такое угол между диагоналями прямоугольника?
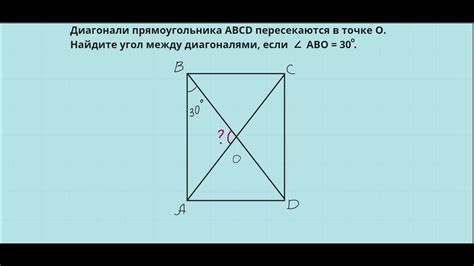
Угол между диагоналями прямоугольника можно найти с помощью математических формул и теорем.
Формула для вычисления угла между диагоналями

Угол между диагоналями прямоугольника может быть найден с использованием теоремы косинусов. Формула для вычисления угла между диагоналями выглядит следующим образом:
Угол = arccos((a^2 + b^2 - c^2) / (2ab))
Где:
- a и b - длины сторон прямоугольника
- c - длина диагонали прямоугольника
- arccos - обратная функция косинуса, возвращает значение угла в радианах
Для использования этой формулы необходимо знать значения длин сторон прямоугольника и длину его диагонали. Зная эти значения, можно подставить их в формулу и выполнить вычисления для определения угла между диагоналями.
Пример:
Пусть у нас есть прямоугольник со сторонами длиной 4 см и 6 см. Найдем угол между его диагоналями.
Длина диагонали прямоугольника может быть найдена с помощью теоремы Пифагора: c = sqrt(a^2 + b^2)
Подставим значения длин сторон в эту формулу: c = sqrt(4^2 + 6^2) = sqrt(16 + 36) = sqrt(52) ≈ 7.211
Теперь можем использовать формулу для пересчета угла: Угол = arccos((4^2 + 6^2 - 7.211^2) / (2 * 4 * 6))
Вычислим значение угла: Угол = arccos((16 + 36 - 52) / 48) ≈ arccos(0.333)
Используя калькулятор, получим:
Угол ≈ 71.6°
Таким образом, угол между диагоналями прямоугольника с данными сторонами составляет примерно 71.6°.
Принцип работы формулы
Для нахождения угла между диагоналями прямоугольника можно использовать формулу, основанную на теореме косинусов.
Формула имеет следующий вид:
Угол = arccos((a^2 + b^2 - c^2) / (2ab))
Где:
- a и b - длины сторон прямоугольника;
- c - длина диагонали прямоугольника.
Для использования этой формулы необходимо знать длины сторон прямоугольника и длину его диагонали. После подстановки соответствующих значений в формулу, можно вычислить значение угла.
Например, пусть у нас есть прямоугольник со сторонами 6 и 8, а длина его диагонали равна 10. Для нахождения угла между диагоналями, подставим значения в формулу:
Угол = arccos((6^2 + 8^2 - 10^2) / (2 * 6 * 8))
Вычисляя это выражение, получаем:
Угол = arccos((36 + 64 - 100) / 96)
Угол = arccos(0.00833333)
Используя калькулятор или математическое ПО, получаем значение угла, равное примерно 89.9 градусов.
Таким образом, применяя формулу, можно найти угол между диагоналями прямоугольника на основе длин его сторон и диагонали.
Пример вычисления угла между диагоналями

Угол между диагоналями можно выразить следующим образом:
угоĒ = arccos((AD^2 + BC^2 - AC^2) / (2 * AD * BC))
Где:
AD и BC - длины диагоналей;
AC - длина боковой стороны прямоугольника.
При вычислении угла между диагоналями важно помнить, что значения диагоналей и сторон должны быть в одной и той же системе измерения (например, в сантиметрах или дюймах).
Давайте посмотрим на пример:
Пусть длина диагонали AB прямоугольника равна 5 см, а длина диагонали CD - 8 см. Также известно, что боковая сторона AC равна 3 см.
Подставим данные в формулу:
угоĒ = arccos((3^2 + 8^2 - 5^2) / (2 * 3 * 8))
угоĒ = arccos((9 + 64 - 25) / 48)
угоĒ = arccos(48 / 48)
угоĒ = arccos(1)
Угол между диагоналями составляет 0 радиан. В данном случае прямоугольник является квадратом, и его диагонали перпендикулярны друг другу.
Таким образом, пример показывает, как вычислить угол между диагоналями прямоугольника с использованием теоремы косинусов. Эта формула может быть использована для вычисления угла между диагоналями любого прямоугольника с известными значениями длин диагоналей и сторон.
Варианты использования угла между диагоналями

Угол между диагоналями прямоугольника может быть использован в различных областях и задачах. Ниже приведены некоторые варианты использования данного угла:
1. Геометрия и треугольники: Угол между диагоналями может быть использован при решении задач на построение или вычисление параметров треугольников. Например, при нахождении площади треугольника по двум сторонам и углу между ними.
2. Физика и механика: В механике и физике угол между диагоналями может играть роль при анализе равновесия объектов или определении сил, действующих на систему. Например, при определении направления сил, действующих на блок, связанный с натянутыми струнами.
3. Архитектура и строительство: При планировании и проектировании зданий и сооружений угол между диагоналями может использоваться для определения соответствия прямоугольности конструкции или контроля перпендикулярности углов.
4. Геодезия и картография: В геодезии и картографии угол между диагоналями может использоваться для вычисления проекций плоских карт или определения истинных координат объектов на местности.
5. Робототехника и автоматизация: В робототехнике и автоматизации угол между диагоналями может использоваться для определения ориентации робота или корректировки траектории движения.
Это лишь некоторые примеры использования угла между диагоналями прямоугольника. В зависимости от конкретной задачи или области применения, данный угол может играть различные функциональные роли.
Решение задачи с помощью программы
Для решения данной задачи можно написать программу, которая будет вычислять угол между диагоналями прямоугольника на основе данных о его сторонах.
Возьмем стороны прямоугольника и обозначим их переменными a и b. Для удобства дальнейших вычислений, будем считать, что стороны прямоугольника задаются в виде положительных чисел.
Диагонали прямоугольника можно найти с помощью теоремы Пифагора. Для этого нужно возвести каждую сторону в квадрат, сложить полученные значения и извлечь корень квадратный из суммы. Обозначим диагонали переменными d1 и d2.
Угол между диагоналями можно найти с помощью косинуса угла. Для этого нужно найти косинус угла, зная значения сторон прямоугольника и диагональ. Обозначим угол переменной angle.
Программа для решения задачи может выглядеть следующим образом:
a = float(input("Введите длину стороны a: "))
b = float(input("Введите длину стороны b: "))
d1 = ((a ** 2) + (b ** 2)) ** 0.5
d2 = ((a ** 2) + (b ** 2)) ** 0.5
angle = math.degrees(math.acos((2 * (a ** 2) + (b ** 2) - (d2 ** 2)) / (2 * a * b)))
print("Угол между диагоналями прямоугольника равен", round(angle, 2), "градусов.")Выполнив эту программу, вы получите значение угла в градусах между диагоналями прямоугольника.
Пример:
Введите длину стороны a: 3
Введите длину стороны b: 4
Угол между диагоналями прямоугольника равен 90.0 градусов.




