Математика – это наука, которая исследует свойства и взаимоотношения чисел, пространства и форм. Среди основных понятий математики – функция. Функция – это зависимость одного набора чисел от другого. Изучая функции, очень полезно уметь описывать их свойства по графику. График функции даёт нам интуитивное представление о её поведении в зависимости от изменения аргумента.
Описание свойств функции по графику – это процесс изучения её основных особенностей, таких как возрастание, убывание, максимумы и минимумы, асимптоты и периодичность. Анализируя график функции, мы можем получить информацию о том, как функция ведёт себя на разных участках оси, а также о границах её изменения и возможных точках экстремума.
Для описания свойств функции по графику важно использовать язык математики. При помощи особых терминов и обозначений можно точно формулировать выводы и делать достоверные утверждения. Например, для определения возрастания или убывания функции, используют понятия производной и производной функции.
Как делать описание свойств функции по графику? Важно внимательно рассмотреть график функции, обратить внимание на все особенности и необычности. Затем провести анализ поэтапно, используя различные методы и приёмы математического анализа. В ходе анализа необходимо сделать выводы и проверить их на соответствие математическим правилам и определениям.
В заключение, описание свойств функции по графику – это важный инструмент для анализа её поведения и поиска решений различных задач. Умение описывать свойства функции по графику позволяет нам исследовать и понять её характеристики без использования сложных вычислений и формул.
Декодирование свойств функции по графику: ключевые этапы и их значение
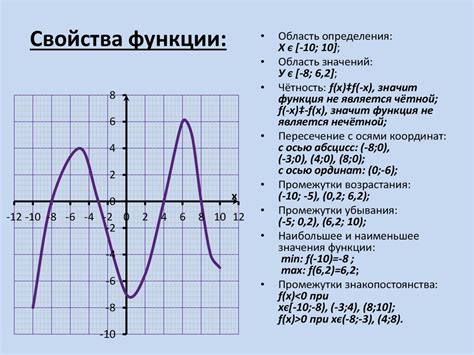
Первым этапом декодирования графика функции является определение области определения. Область определения представляет собой множество всех значений аргумента, для которых функция определена. Для этого необходимо определить, на каких участках оси абсцисс имеется график функции и где он прерывается.
Вторым ключевым этапом является определение области значений функции. Область значений функции представляет собой множество всех значений функции на оси ординат. Для этого необходимо определить, какие значения принимает функция на каждом участке оси абсцисс и где возможны разрывы и асимптоты.
Третий этап связан с определением монотонности функции. Монотонность функции указывает на то, в каком направлении изменяются значения функции на протяжении всей области определения. Для этого необходимо определить, является ли функция возрастающей, убывающей или имеет точки экстремума.
Четвертый этап связан с определением поведения функции на различных участках оси абсцисс. На этом этапе необходимо определить, как функция ведет себя на участках, где график функции имеет вертикальные и горизонтальные асимптоты, разрывы и особые точки. Также нужно обратить внимание на наличие пересечений с осями координат.
Таким образом, декодирование свойств функции по графику включает несколько ключевых этапов: определение области определения, области значений, монотонности и поведения функции на различных участках оси абсцисс. Каждый из этих этапов играет важную роль в анализе функций и позволяет получить более полное представление о свойствах данной функции.
Процесс разбора графика функции: на что обратить внимание
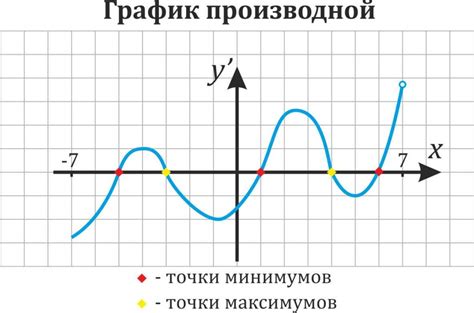
Когда мы анализируем график функции, важно обратить внимание на несколько ключевых аспектов, чтобы правильно понять свойства этой функции. Вот что стоит отметить:
1. Значения функции: График функции показывает, какие значения принимает функция в зависимости от значения аргумента. Обратите внимание на точки, где значение функции равно нулю, так как они могут указывать на корни уравнения. Также учтите, что функция может иметь экстремумы, то есть максимумы и минимумы.
2. Поведение функции: На графике можно определить, как функция изменяется во всей области определения. Обратите внимание на наличие асимптот или особых точек, таких как разрывы функции или точки разрыва.
3. Монотонность: График функции может быть возрастающим или убывающим на определенных интервалах. При анализе графика обратите внимание на возможные точки перегиба, где функция меняет свой характер.
4. Симметрия: Функция может быть симметричной относительно оси y или оси x. Обратите внимание на наличие симметричных точек или осей, так как они могут указывать на определенные свойства функции.
5. Ограничения функции: При анализе графика обратите внимание на любые ограничения, которые могут существовать для функции. Например, функция может быть определена только на определенном интервале или ограничена сверху или снизу.
Анализ графика функции требует внимательности и умения обратить внимание на детали. Используйте эти ключевые аспекты, чтобы получить более полное представление о свойствах функции и сделать более точные выводы.
Практические рекомендации по анализу графика функции: как получить полный обзор
Для получения полного обзора графика функции следует придерживаться следующих рекомендаций:
1. Определить область определения функции: область, в которой функция определена, определяет множество значений аргумента, на которых график будет строиться. Необходимо обратить внимание на исключения, такие как деление на ноль или на отрицательное число.
2. Найти особые точки и интервалы: особые точки, такие как нули функции или точки, где функция не определена, могут указывать на особенности графика, такие как экстремумы или разрывы.
3. Задать значения функции в критических точках: критические точки, где производная функции равна нулю или не существует, часто являются местами максимума или минимума функции. Задав значения функции в этих точках, можно получить информацию о поведении графика в окрестности этих точек.
4. Исследовать поведение графика в окрестности точек пересечения с осями: пересечения с осями координат могут указывать на нули функции или наличие асимптот.
5. Анализировать график на предмет монотонности и экстремумов: узнать, возрастает или убывает функция в разных интервалах, и найти точки максимума и минимума.
6. Проверить наличие периодичности: если функция является периодической, то это будет отражено в графике. Необходимо обратить внимание на повторяющиеся интервалы или паттерны.
7. Изучить наличие асимптот: асимптоты графика функции могут указывать на поведение функции в бесконечности или близости к определенным значениям. Они могут быть вертикальными, горизонтальными или наклонными.
Следуя этим практическим рекомендациям, вы сможете получить полный обзор о свойствах функции, анализируя её график. Это поможет вам лучше понять и использовать функцию в различных математических и физических задачах.




