Разложение многочлена по степеням двучлена - это процесс приведения многочлена к виду, в котором его можно представить в виде суммы произведений двучленов. Это основная операция в алгебре и позволяет упростить выражение и получить его более компактную запись. Разложение многочлена основывается на применении законов алгебры, включая раскрытие скобок, сортировку мономов по степеням и сбор подобных членов.
Для начала необходимо определить, что такое двучлен. Двучлен - это алгебраическое выражение, состоящее из двух слагаемых (мономов), соединенных знаком "+" или "-". Примером двучлена может быть выражение x + y или а - 2b. Для разложения многочлена по степеням двучлена необходимо привести его к такому виду, чтобы каждый его моном был двучленом.
Пример:
Разложим многочлен 3x^2 + 5xy - 2y^2 + 4x - 3y по степеням двучлена.
Сначала сортируем мономы по степеням. Получаем: 3x^2 - 2y^2 + 5xy + 4x - 3y.
Затем группируем мономы с одинаковыми степенями. Поскольку все мономы являются двучленами, нет необходимости объединять их внутри скобок. Получаем: (3x^2) + (-2y^2) + (5xy) + (4x) + (-3y).
В результате разложение многочлена по степеням двучлена имеет вид: 3x^2 - 2y^2 + 5xy + 4x - 3y.
Таким образом, разложение многочлена по степеням двучлена позволяет представить выражение в виде суммы двучленов и упростить его. Это важный навык, который может быть полезен в решении различных алгебраических задач и упрощении сложных выражений.
Основные принципы разложения многочлена по степеням двучлена
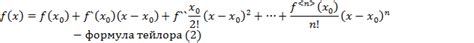
Основная идея разложения многочлена по степеням двучлена состоит в том, чтобы факторизовать общий двучлен, вынести его за скобки и привести подобные члены внутри этих скобок. Процесс разложения сопровождается последовательным применением правил алгебры, включая раскрытие скобок, сочетание подобных членов и сортировку по степеням переменной.
Например, рассмотрим многочлен 4x^2y - 2xy^2 + 6xy - 3x^2 - 4y^2 + 2x - 3y. Для разложения по степеням двучлена, сначала можно выделить общий двучлен для каждой группы членов: x и y. Затем проводим факторизацию, вынося общий двучлен за скобки: x(4x-3) + y(6x-2-4y)-3y. И, наконец, приводим подобные члены внутри скобок и упорядочиваем по степеням переменных: 4x^2-3x + 6xy-2y-4y^2-3y.
Примеры разложения многочлена по степеням двучлена
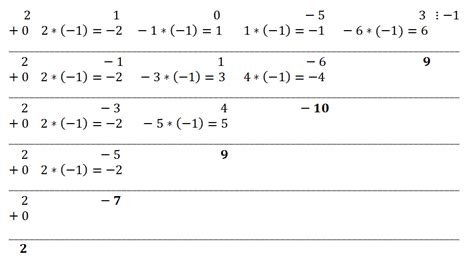
Для лучшего понимания процесса разложения многочлена по степеням двучлена, рассмотрим несколько примеров:
Пример 1:
Разложим многочлен 3x2 + 8x + 4.
Мы видим, что первый член является квадратом двучлена x. Это означает, что получился квадратный трехчлен. Теперь нам нужно разложить двучлен 8x + 4.
Можно заметить, что двучлен 8x + 4 также является квадратным трехчленом. Поэтому разложение можно записать следующим образом:
3x2 + 8x + 4 = (x + 2)(x + 2)
Пример 2:
Разложим многочлен 2x2 - 9x + 5.
В данном случае первый член также является квадратом двучлена x, а второй член - линейным трехчленом. Разложение будет выглядеть следующим образом:
2x2 - 9x + 5 = (x - 5)(x - 1)
Пример 3:
Разложим многочлен 4x2 - 12x + 9.
В этом примере первый член снова является квадратом двучлена x, а второй член является линейным трехчленом. Разложение будет иметь вид:
4x2 - 12x + 9 = (2x - 3)(2x - 3)
Это только некоторые примеры разложения многочлена по степеням двучлена. Надеюсь, что они помогут вам лучше понять этот процесс.




