Формулировка теоремы - это способ выражения основных идей и результатов в математике. Зачастую, теоремы используются для доказательства или объяснения определенных математических фактов или явлений.
Основными понятиями формулировки теоремы являются условие теоремы и вывод теоремы. Условие теоремы - это предположение или набор предположений, которые необходимо выполнить, чтобы доказать или использовать теорему. Вывод теоремы - это утверждение или последовательность утверждений, которые следуют из условия теоремы.
Основные принципы формулировки теоремы включают ясность, точность и строгость. Ясность формулировки теоремы позволяет легко понять и интерпретировать ее основные идеи. Точность формулировки теоремы обеспечивает отсутствие двусмысленности и позволяет четко сформулировать условие и вывод теоремы. Строгость формулировки теоремы требует строгой логики и формальных определений, чтобы избежать ошибок или недостатка в доказательстве или использовании теоремы.
Важно отметить, что формулировка теоремы является ключевым аспектом в математике и играет важную роль в разработке новых теорий, решении математических задач и продвижении существующих теорий и идей.
В заключение, формулировка теоремы представляет собой средство выражения основных идей и результатов в математике, используется для доказательства или объяснения математических фактов и явлений. Она состоит из условия и вывода теоремы, требует ясности, точности и строгости для правильного понимания и использования. Формулировка теоремы имеет важное значение в математике и способствует развитию новых теорий и решению математических задач.
Основные понятия формулировки теоремы

Основные понятия формулировки теоремы включают:
| Термин | Определение |
|---|---|
| Функция | Отображение множества элементов одного множества в другое множество, где каждому элементу из первого множества сопоставляется один элемент из второго множества. |
| Числовой аргумент | Число, подставляемое в функцию в качестве входного значения. |
| Утверждение | Аксиома или простое высказывание, имеющее значение истинности или ложности. |
| Нечетность | Свойство числа быть нечетным, то есть не делиться на 2 без остатка. |
Формулировка теоремы является основой для дальнейшего доказательства и изучения свойств числовых функций от вещественного аргумента.
Формулировка

Условие теоремы содержит набор предположений или ограничений, которые необходимо выполнить, чтобы применить теорему. Оно дает контекст и описывает ситуацию, в которой применяется теорема.
Заключение теоремы, с другой стороны, представляет собой утверждение, которое делается на основе условий. Оно содержит результат или вывод, который может быть получен из применения теоремы.
Формулировка теоремы должна быть ясной, однозначной и точной, чтобы исключить возможность двусмысленности или неправильной интерпретации. Она является основой для понимания сути теоремы и дает направление для доказательства или применения.
Теорема
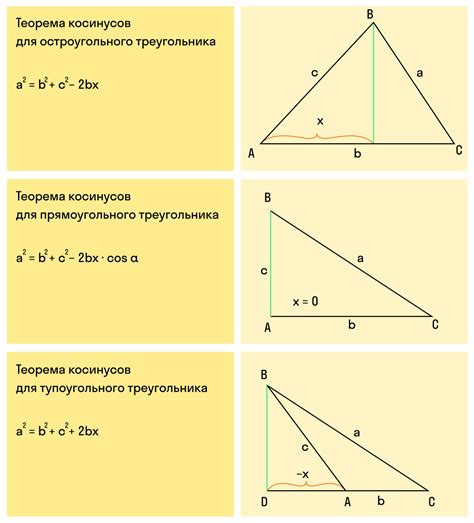
Формулировка теоремы должна быть четкой и точной, чтобы ее можно было однозначно понять и проверить. Обычно она состоит из двух частей: условия и вывода. Условие содержит данные, на основе которых делается вывод. Вывод содержит утверждение или следствие, которое является результатом рассуждений и доказательств.
Пример формулировки теоремы: "Теорема Пифагора: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов".
Теоремы являются фундаментальными элементами математического знания и играют важную роль в доказательствах и исследованиях. Они позволяют установить новые факты, связи и закономерности, а также применять математические знания на практике.
| Теорема | Условие | Вывод |
|---|---|---|
| Теорема Пифагора | В прямоугольном треугольнике | Квадрат длины гипотенузы равен сумме квадратов длин катетов |
Основные понятия
Условие - это начальные данные или предположения, которые принимаются в теореме. Условие определяет предмет исследования, обозначает весь набор предпосылок, которые нужны для доказательства.
Заключение - это утверждение, которое следует из условия. В теореме заключение является основным результатом, который необходимо доказать.
Понятие - это обобщенное представление о предмете исследования. Оно позволяет обозначить класс объектов, которые имеют схожие свойства или способность выполнять определенные действия.
Принцип - это общая идея или метод, который лежит в основе теоремы или доказательства. Принцип определяет логику и шаги, которые нужно выполнить для получения желаемого результата.
Принципы
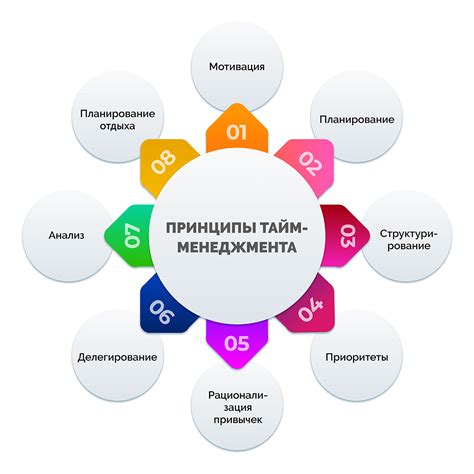
В математике формулировки теорем основаны на определенных принципах, которые помогают структурировать и объяснить математические концепции и их взаимосвязи. Вот несколько основных принципов, которые применяются при формулировке теорем:
- Принцип непротиворечивости - формулировка теоремы должна быть логически согласованной и не противоречить другим математическим аксиомам и теориям.
- Принцип достаточности - формулировка теоремы должна быть достаточно конкретной и точной, чтобы математикам было понятно, что именно утверждается.
- Принцип единственности - формулировка теоремы должна быть единственной и не допускать неоднозначных толкований или различных интерпретаций.
- Принцип обратимости - формулировка теоремы должна быть обратимой, то есть иметь возможность быть доказанной и доказательство должно обратиться: если теорема доказана, то она верна, и наоборот.
- Принцип связности - формулировка теоремы должна быть взаимосвязанной с другими математическими понятиями и теориями, чтобы ее можно было использовать в дальнейших исследованиях и применениях.
Эти принципы помогают ученым создавать четкие и точные формулировки теорем, которые могут быть проверены и использованы в различных математических областях.




