Проверка уравнения является важным шагом при решении математических задач. Она позволяет убедиться в правильности полученного результата и исключить возможные ошибки при выполнении операций. В этой статье мы рассмотрим несколько примеров и разберем процесс выполнения проверки уравнения.
Проверка уравнения осуществляется путем подстановки найденных значений переменных обратно в исходное уравнение и проверки равенства обеих частей уравнения. Если результат проверки соответствует исходному уравнению, то это означает, что наш решение является верным.
Например, рассмотрим уравнение 2x + 3 = 7. После проведения необходимых операций, мы получаем x = 2. Чтобы проверить правильность нашего решения, подставим найденное значение x = 2 в исходное уравнение: 2 * 2 + 3 = 7. После выполнения вычислений получаем 4 + 3 = 7, что действительно равно 7. Таким образом, мы убеждаемся, что наше решение верно.
Выполнение проверки уравнения особенно важно при решении сложных задач, где имеется множество операций и шагов. Это позволяет избежать ошибок, которые могут возникнуть при неправильном выполнении вычислений или при использовании неправильных значений переменных. Благодаря проверке уравнения, мы можем быть уверены в правильности нашего решения и дальше приступать к следующим шагам или задачам.
В заключение, выполнение проверки уравнения является важной частью процесса решения задач по математике. Она позволяет убедиться в правильности полученного результата и избежать возможных ошибок. Рекомендуется всегда проводить проверку уравнения, особенно при решении сложных задач. Это поможет сохранить точность и достоверность наших вычислений.
Зачем проверять уравнения
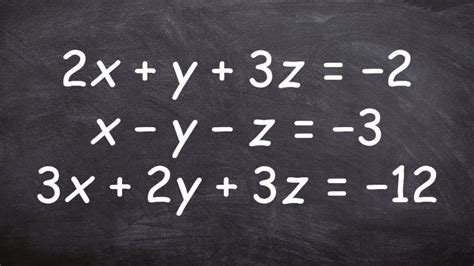
Проверка уравнения обычно выполняется путем подстановки найденных значений переменных обратно в исходное уравнение и проверки равенства обеих частей. Если равенство выполняется, то решение верно. В противном случае, необходимо проверить предыдущие шаги решения и исправить возможные ошибки.
Проверка уравнений также позволяет проверить правильность работы использованных математических операций и свойств, что способствует развитию навыков решения математических задач.
Важность проверки уравнений

Проверка уравнения заключается в подстановке найденных значений переменных в исходное уравнение и сравнению полученных результатов с правой и левой частью уравнения. Если обе части уравнения равны, то полученное решение корректно.
Проверка уравнений особенно важна в случаях, когда решение может содержать подразумеваемые допущения или случайные ошибки. Также проверка позволяет избежать возможных неполадок при дальнейших вычислениях или использовании решения в других задачах.
При проведении проверки уравнений необходимо быть внимательным и аккуратным, чтобы не допустить ошибок при подстановке значений и выполнении арифметических операций. Также следует учитывать особенности уравнения и возможные случаи исключений.
В заключение, проверка уравнений является неотъемлемой частью решения задач и помогает гарантировать правильность полученного решения. Правильная проверка позволяет избежать ошибок и увеличить точность математических вычислений.
Примеры уравнений и их решение

В данном разделе рассмотрим несколько примеров уравнений и способы их решения.
Пример 1: Решение квадратного уравнения
Дано уравнение: 2x^2 + 5x - 3 = 0
Для решения данного уравнения можно использовать квадратное уравнение вида ax^2 + bx + c = 0
- Сначала найдём дискриминант по формуле: D = b^2 - 4ac
- Если D > 0, то уравнение имеет два различных корня x1 и x2, которые можно найти по формуле: x1,2 = (-b ± √D) / (2a)
- Если D = 0, то у уравнения есть только один корень, который можно найти по формуле: x = -b / (2a)
- Если D , то у уравнения нет действительных корней.
Для данного примера, дискриминант равен: D = 5^2 - 4 * 2 * (-3) = 49
Так как D > 0, то у уравнения есть два корня.
Подставляя значения в формулу, получаем:
x1,2 = (-5 ± √49) / (2 * 2) = (-5 ± 7) / 4
Таким образом, уравнение имеет два корня: x1 = 1 и x2 = -3/2.
Пример 2: Решение линейного уравнения
Дано уравнение: 3x - 2 = 7
Для решения данного уравнения достаточно выразить переменную x.
Перенесём константу на другую сторону уравнения:
3x = 7 + 2
3x = 9
Разделим обе части уравнения на коэффициент перед x:
x = 9 / 3
x = 3
Таким образом, решение уравнения 3x - 2 = 7 равно x = 3.
Пример 3: Решение кубического уравнения
Дано уравнение: x^3 - 6x^2 + 11x - 6 = 0
Для решения данного уравнения можно использовать различные методы, например, метод графического вывода или метод Ньютона.
В данном случае, можно заметить, что уравнение имеет один корень x = 1. Выполнив деление уравнения на x - 1, получим:
x^2 - 5x + 6 = 0
Это уже квадратное уравнение, которое мы уже знаем, как решать. Применяя метод решения квадратного уравнения из примера 1, получим два корня: x1 = 2 и x2 = 3.
Таким образом, решение кубического уравнения x^3 - 6x^2 + 11x - 6 = 0 равно x = 1, 2, 3.




