Круги Эйлера - это важный концепт в теории множеств. Эти круги широко используются в математике и информатике для обозначения взаимосвязи между множествами. Идея была впервые предложена Леонардом Эйлером, великим швейцарским математиком 18 века.
Круги Эйлера состоят из пересекающихся окружностей, каждая из которых представляет собой отдельное множество. Области пересечения окружностей представляют собой взаимные включения между множествами. Таким образом, с помощью кругов Эйлера можно наглядно показать смысл пересечения и объединения множеств.
Зачем же нужны круги Эйлера? Эти диаграммы позволяют визуально представить сложные отношения между множествами и сделать выводы о том, какие элементы принадлежат различным категориям. Они помогают организовать информацию и сделать ее легко понятной для людей. Круги Эйлера также пригодны для анализа данных и вычисления вероятности.
Круги Эйлера - это мощный инструмент, который позволяет наглядно представить сложные отношения между множествами и делает математические концепции доступными для широкого круга людей.
Значение и назначение Кругов Эйлера

Круги Эйлера, введенные Леонардом Эйлером в XVIII веке, имеют большое значение в различных областях математики и науки. Назначение этих графических представлений заключается в иллюстрации взаимосвязей между множествами или группами элементов.
Одним из основных применений Кругов Эйлера является категоризация данных. Они позволяют группировать элементы по определенным признакам и наглядно показывают, какие элементы принадлежат одновременно к нескольким категориям и какие уникальны для каждой категории.
Круги Эйлера также используются в логике и теории множеств. Они помогают исследовать пересечения и отношения между группами объектов, а также устанавливать свойства множеств. С их помощью можно решать задачи на нахождение объединений, пересечений, разницы множеств и других операций.
Круги Эйлера активно применяются также в биологии, экологии, социологии и других науках. Они помогают описывать структуру и связи между различными объектами или явлениями, проводить классификацию и анализ данных, определять сходства и различия между образцами и многое другое.
В современной информационной технологии и разработке программного обеспечения Круги Эйлера интенсивно используются для визуализации и анализа сложных данных, таких как социальные сети, графы связности, базы данных и т.д. Они помогают упростить восприятие информации и выделить основные взаимосвязи.
Таким образом, Круги Эйлера имеют значительное значение и широкое применение в различных науках и практических областях. Они помогают наглядно представлять и систематизировать информацию, а также выявлять связи и взаимодействия между объектами и явлениями.
История создания Кругов Эйлера
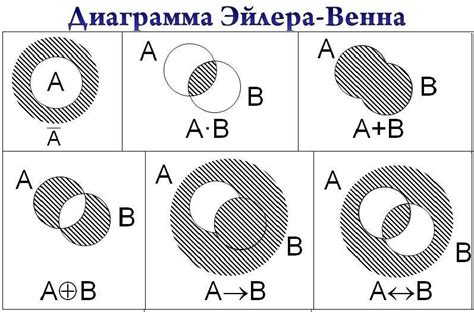
Идея о представлении математических отношений и связей с помощью диаграмм впервые возникла в голове швейцарского математика и физика Леонарда Эйлера в XVIII веке. В то время он работал над проблемой семей источников рек и речных островов.
В своих исследованиях Эйлер разработал графический метод, который позволял наглядно представлять связи между различными объектами. Он использовал кольца, которые олицетворяли различные группы объектов, и линии, которые обозначали отношения между этими группами.
Со временем этот метод стал известен как "круги Эйлера" и нашел широкое применение в различных областях знания. Математики использовали круги Эйлера для визуализации отношений между множествами, компьютерные ученые применяют их для анализа данных и биологи - для изучения генетических связей.
Сегодня круги Эйлера стали неотъемлемой частью нашей жизни. Мы видим их во множестве областей - от медицинских исследований до маркетинговых анализов. Они позволяют нам наглядно представлять сложные отношения и сделать выводы, которые могут служить основой для принятия решений.
Определение и особенности Кругов Эйлера
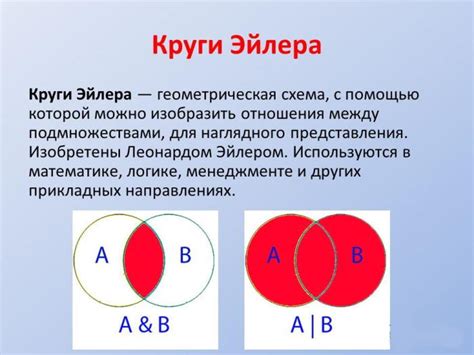
Круги Эйлера представляют собой пересекающиеся области на плоскости, каждая из которых представляет отдельное множество. Круги отображаются в виде эллипсов или окружностей, причем их пересечения показывают наличие общих элементов между множествами.
Основное назначение Кругов Эйлера - наглядно иллюстрировать наборы и отношения между множествами. Эти круги широко применяются в различных областях знаний, таких как математика, логика, информатика, статистика и другие.
Круги Эйлера имеют несколько особенностей, которые делают их полезными в визуализации данных. Во-первых, внешние границы каждого круга указывают на четкое разделение множеств. Во-вторых, пересечение кругов показывает наличие общих элементов между множествами, а размер пересечения отражает количество общих элементов. В-третьих, построение Кругов Эйлера позволяет определить объединение и пересечение множеств, а также их разницу. Поэтому Круги Эйлера являются мощным инструментом для анализа данных и понимания логических отношений.
| Множество A | Множество B | Пересечение A и B | Объединение A и B | Разность A и B | |
|---|---|---|---|---|---|
| Круг Эйлера | Область A | Область B | Пересекающая область | Область A и B | Область A без общих элементов B |
Применение Кругов Эйлера в математике
Один из основных способов применения Кругов Эйлера в математике - это исследование пересечений множеств. Круги Эйлера помогают наглядно представить, какие элементы принадлежат одному, нескольким или всем из заданных множеств. Это значительно упрощает работу с задачами, связанными с логическими операциями, такими как объединение, пересечение и разность множеств.
Круги Эйлера также часто применяются в комбинаторике. Они позволяют наглядно представить количество различных комбинаций, подмножеств и перестановок элементов. Например, с их помощью можно проиллюстрировать, сколько существует различных комбинаций букв в слове или различных групп предметов.
Круги Эйлера также находят применение в теории множеств и логике. Они используются для изображения отношений между множествами, подмножествами и подпространствами. Кроме того, Круги Эйлера широко применяются для визуализации логических операций, таких как импликация, эквивалентность и противоположность.
В конечном счете, Круги Эйлера являются мощным инструментом не только в математике, но и в других областях. Они могут быть использованы для анализа данных, управления проектами, принятия решений, а также для облегчения понимания сложных концепций и взаимосвязей.
Важность Кругов Эйлера в информационной технологии
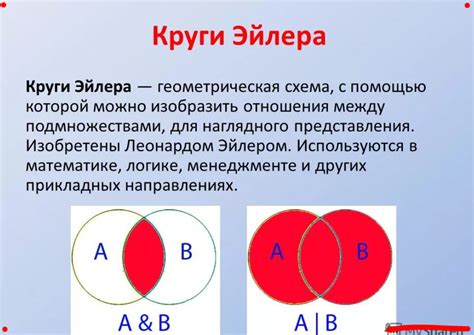
Круги Эйлера представляют собой графическое представление информации с использованием пересекающихся окружностей. В информационной технологии они играют важную роль.
Первое и самое очевидное применение Кругов Эйлера - визуализация пересечений и совпадений множеств. Используя этот метод, ученые, программисты и аналитики могут легко представить, какие элементы принадлежат к различным множествам и какие элементы пересекаются между множествами. Это упрощает анализ данных и обнаружение шаблонов, что в свою очередь помогает принимать более эффективные и обоснованные решения.
Круги Эйлера также широко применяются в контексте баз данных и программного обеспечения. Они могут быть использованы для визуализации связей между различными таблицами базы данных, что позволяет легче понять схему данных и взаимосвязи между таблицами. Это помогает разработчикам создавать более эффективные и оптимизированные базы данных.
Кроме того, Круги Эйлера могут быть использованы для визуализации алгоритмов в информационной технологии. Они помогают понять, какие шаги алгоритма перекрываются или пересекаются друг с другом, что может помочь в оптимизации алгоритма и улучшении его производительности.
В целом, использование Кругов Эйлера в информационной технологии позволяет сделать сложные данные более наглядными и понятными. Этот метод визуализации помогает аналитикам и разработчикам обрабатывать, анализировать и интерпретировать данные более эффективно, что в конечном итоге способствует принятию более обоснованных и качественных решений.




