Цифра, расположенная над корнем в математике, играет важную роль в определении порядка корня. В математических выражениях, в которых присутствуют корни, значение цифры над корнем определяет степень корня. Это важно для правильного решения уравнений и построения графиков функций.
Пример: Если у нас есть корень n-ой степени из числа а, обозначаемый как √a, то цифра n, расположенная над корнем, указывает на степень корня. Например, если у нас есть корень квадратный, то n будет равно 2.
Знание значения цифры над корнем особенно полезно при решении уравнений, содержащих корни разных степеней. Это поможет нам правильно определить количество решений и найти их точные значения.
Понимание значения цифры над корнем также позволяет нам конкретизировать изображение графика функции. Численное значение n может менять форму и направление графика, что особенно важно при анализе поведения функций при различных значениях переменных.
Что означает цифра над корнем в математике?
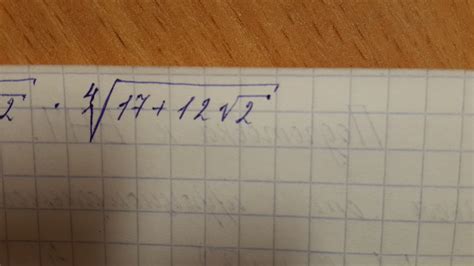
В математике цифра над корнем обозначает степень корня. Когда перед корнем указывается цифра, это означает, что корень берется из данного числа в указанной степени.
Например, если перед корнем стоит цифра 2, это значит, что берется квадратный корень. То есть, чтобы найти значение выражения, нужно из указанного числа извлечь квадратный корень.
Запись с цифрой над корнем может выглядеть следующим образом:
√a , где a - число, из которого берется корень.
Например, если написано √16, это означает, что из числа 16 нужно извлечь корень. Если перед корнем стоит цифра 2, то значение выражения будет равно 4, так как 4 в квадрате равно 16.
Цифра над корнем также может быть другой, например 3 или 4, что означает, что берется кубический корень или корень четвертой степени соответственно.
Знание значения цифры над корнем может быть полезным при решении различных математических задач и вычислении значений выражений.
Пояснение и примеры

Цифра, стоящая над корнем в математике, обозначает степень корня. То есть, она показывает, в какую степень возводится число под корнем.
Например:
- √2 означает квадратный корень, то есть число, которое возведенное в квадрат дает 2. Таким числом будет √2 = 1,4142...
- ∛3 означает кубический корень, то есть число, которое возведенное в куб дает 3. Таким числом будет ∛3 = 1,4422...
Также, цифра над корнем может указывать на другие степени корня, например:
- ∜4 означает корень четвертой степени, то есть число, которое возведенное в четвертую степень дает 4. Таким числом будет ∜4 = 2
Таким образом, цифра над корнем важна для определения степени корня и помогает нам вычислить значение корня.
Первое значение цифры над корнем
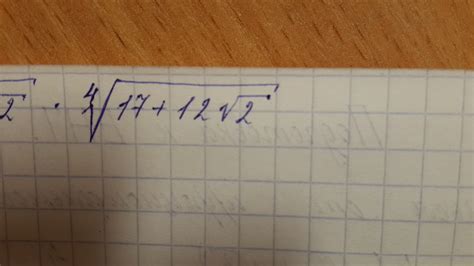
В математике значение цифры над корнем указывает на степень, в которую нужно возвести корень. Если цифра над корнем равна 2, то корень возводится в квадрат. Если цифра равна 3, то корень возводится в куб. И так далее.
Например, если дано уравнение:
√4x
Так как значение цифры над корнем равно 2, то корень возводится в квадрат. Значит, уравнение можно записать так:
4x = 16
Здесь мы возвели корень в квадрат, получили число 16 и решили уравнение, найдя значение переменной x.
Таким образом, значение цифры над корнем является важным элементом в математических выражениях, определяющим степень, в которую нужно возвести корень для решения уравнений.
Второе значение цифры над корнем
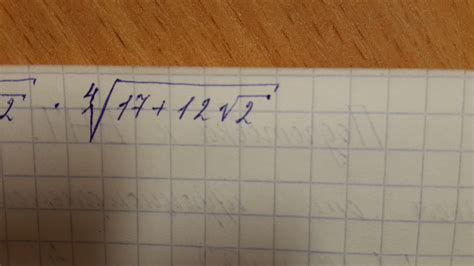
Цифра, расположенная над знаком корня, в математике может иметь второе значение, которое представляет собой показатель степени. Если перед корнем стоит число, и над знаком корня расположена другая цифра, то это означает, что вычисление подкоренного выражения нужно возвести в степень, указанную над корнем.
Например, если в выражении встречается корень второго порядка (√) и над ним располагается цифра 5, то это означает, что подкоренное выражение нужно возвести в пятую степень.
Пример:
√x5 = (x)5
В этом примере, подкоренное выражение (x) будет возведено в степень 5. Таким образом, результатом будет x в пятой степени.
Понимание второго значения цифры над корнем является важным для точного выполнения математических операций и решения уравнений. Для более сложных выражений, в которых встречаются несколько корней или разные показатели степени, правильное определение значений цифр над корнями становится еще более важным.




