Отрицательная степень - это один из важных понятий в математике, которое часто встречается при работе с дробями. Когда мы возведем дробь в отрицательную степень, мы получим результат, равный обратной величине этой дроби, возведенной в положительную степень.
Например, если у нас есть дробь 1/2, и мы возведем ее в отрицательную степень -2, то получим результат, равный (1/2)^(-2) = 2^2/1^2 = 4/1 = 4. То есть, отрицательная степень дроби 1/2 равна 4.
Отрицательная степень для дробей имеет свои правила, которые помогают нам считать ее правильно. Существуют два основных правила: правило отрицательной степени числителя и правило отрицательной степени знаменателя.
Правило отрицательной степени числителя утверждает, что если мы возведем дробь в отрицательную степень, то степень числителя остается такой же, а степень знаменателя станет положительной.
Правило отрицательной степени знаменателя утверждает, что если мы возведем дробь в отрицательную степень, то степень знаменателя остается такой же, а степень числителя станет положительной.
Использование этих правил позволяет нам с легкостью рассчитывать отрицательные степени для дробей и получать правильный результат.
Отрицательная степень: что это такое?

Для примера, если у нас есть дробь 1/2 и мы возводим ее в степень -1, то получаем следующее выражение: (1/2)^(-1). В результате получаем 2/1, что эквивалентно числу 2. Таким образом, отрицательная степень позволяет нам найти обратную дробь в числовом виде.
Отрицательная степень имеет несколько основных правил, которые позволяют выполнять эту операцию. Например, если у нас есть дробь a/b и мы возводим ее в степень -n, то результат можно получить следующим образом: (a/b)^(-n) = (b/a)^n. Это правило позволяет нам переставить числитель и знаменатель местами и изменить знак степени.
Определение отрицательной степени для дробей
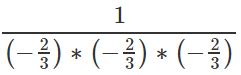
Для более полного понимания можно рассмотреть пример. Пусть у нас есть дробь 2/3 и нам нужно возвести ее в отрицательную степень -2. Согласно определению, отрицательная степень этой дроби будет равна обратной величине положительной степени этой же дроби. То есть 2/3-2 = (3/2)2 = 9/4.
Таким образом, отрицательная степень для дробей может быть вычислена путем взятия обратной величины положительной степени этой же дроби.
Правила умножения и деления дробей в отрицательной степени
При работе с отрицательными степенями дробей, существуют специальные правила для выполнения умножения и деления. Эти правила позволяют нам более удобно работать и упрощать такие выражения.
Правило умножения:
Для умножения двух дробей в отрицательной степени, мы перемножаем числители и знаменатели отдельно. Затем мы меняем знак степени на противоположный.
Например, если у нас есть выражение a/b в отрицательной степени, и мы хотим умножить его на выражение c/d в отрицательной степени, то результат будет:
(a/b) * (c/d) = (a * c) / (b * d)
Первоначально мы получаем дробь с числителем равным произведению числителей и знаменателей исходных дробей. Затем мы меняем знак степени на противоположный.
Правило деления:
Для деления двух дробей в отрицательной степени, мы умножаем первую дробь на обратную второй дроби. Затем мы меняем знак степени на противоположный.
Например, если у нас есть выражение a/b в отрицательной степени, и мы хотим разделить его на выражение c/d в отрицательной степени, то результат будет:
(a/b) / (c/d) = (a * d) / (b * c)
Мы умножаем числитель первой дроби на знаменатель второй дроби и затем знаменатель первой дроби на числитель второй дроби. После этого мы меняем знак степени на противоположный.
Знание этих правил упростит вам работу с дробями при выполнении умножения и деления в отрицательной степени.
Примеры вычисления отрицательных степеней дробей

Вычисление отрицательных степеней дробей связано с применением основных правил алгебры. Рассмотрим несколько примеров, чтобы лучше разобраться в этом.
Пример 1:
Рассмотрим дробь 3/4 в степени -2. Для этого мы возводим числитель и знаменатель в отрицательную степень.
Таким образом, 3/4 в степени -2 можно записать как (3/4)^(-2).
Согласно правилу, когда дробь возведена в отрицательную степень, мы меняем числитель и знаменатель местами и берем обратное значение каждого из них.
В данном случае получим: (4/3)^2, что равно 16/9.
Пример 2:
Рассмотрим дробь 1/5 в степени -3. Аналогично предыдущему примеру, мы возводим числитель и знаменатель в отрицательную степень.
Итак, 1/5 в степени -3 можно записать как (1/5)^(-3).
Применяя правило, мы меняем числитель и знаменатель местами и берем обратное значение каждого из них.
В данном случае получим: (5/1)^3, что равно 125.
Пример 3:
Рассмотрим дробь 2/3 в степени -1/2. В этом случае, мы возводим числитель и знаменатель в отрицательную степень, которая является дробной.
Таким образом, 2/3 в степени -1/2 можно записать как (2/3)^(-1/2).
Применяя правило, мы меняем числитель и знаменатель местами и берем обратный корень каждого из них.
В данном случае получим: (√3/2)^1, что равно √3/2.
Таким образом, вычисление отрицательных степеней дробей требует применения правил алгебры, и может зависеть от типа степени и значения дроби.




