Отрицательный критерий Стьюдента — это статистический метод, который используется для проверки гипотезы о значимости различий между двумя выборками. Он является одним из наиболее использованных и надежных статистических критериев и был разработан Уильямом Госсетом в начале XX века.
Суть отрицательного критерия Стьюдента заключается в следующем: если различие между двумя выборками статистически незначимо, то можно отклонить гипотезу об их различии. В противном случае, если различие статистически значимо, гипотезу принимают исходя из эмпирических данных.
Применение отрицательного критерия Стьюдента является существенным во многих областях, таких как медицина, экономика, психология, социология и других. Он позволяет оценить статистическую значимость различий и сделать выводы на основе этих данных.
Отрицательный критерий Стьюдента является мощным инструментом статистического анализа и помогает исследователям делать обоснованные выводы на основе данных. Его использование позволяет проверять гипотезы и определить, является ли различие между выборками статистически значимым или случайным. Результаты, полученные с помощью отрицательного критерия Стьюдента, имеют высокую точность и репрезентативность, что делает его незаменимым инструментом в современном исследовании.
Отрицательный критерий Стьюдента: основные понятия и его значение

В отличие от положительного критерия Стьюдента, который применяется для проверки гипотезы о равенстве средних значений двух выборок, отрицательный критерий Стьюдента применяется для проверки гипотезы о неравенстве этих средних значений.
При применении отрицательного критерия Стьюдента сначала формулируется нулевая гипотеза, согласно которой средние значения выборок равны друг другу. Затем проводится статистический анализ данных, который позволяет определить, насколько сильно средние значения выборок отличаются друг от друга. Если отличие является статистически значимым, то нулевая гипотеза отклоняется, и делается вывод о наличии отрицательного эффекта или различия в отношении изучаемого явления или параметра.
Отрицательный критерий Стьюдента имеет важное значение в научных исследованиях, статистике, медицине, экономике и других областях, где требуется оценивать и сравнивать средние значения выборок. Он позволяет получить объективную оценку статистической значимости различий между выборками и принять обоснованные решения на основе полученных результатов.
Отрицательный критерий Стьюдента: что это такое?

Для применения отрицательного критерия Стьюдента необходимо учитывать следующие шаги:
- Сформулировать нулевую и альтернативную гипотезы. Нулевая гипотеза предполагает, что средние значения двух выборок равны, а альтернативная гипотеза предполагает их неравенство.
- Провести измерения и получить выборки данных.
- Рассчитать значения статистики, основанной на отрицательном критерии Стьюдента. Для этого используются средние значения, стандартные отклонения и размеры выборок.
- Определить критическую область. Значение статистики сравнивается с критическим значением, которое зависит от выбранного уровня значимости – вероятности ошибки первого рода.
- Сделать выводы на основе результатов теста. Если значение статистики попадает в критическую область, то нулевая гипотеза отвергается, что означает наличие статистически значимых различий между выборками. В противном случае, нулевая гипотеза принимается.
Отрицательный критерий Стьюдента широко используется в науке и исследованиях для сравнения двух групп, методов, технологий и других статистических показателей. Он позволяет получить объективные и научно обоснованные результаты и сделать выводы на основе статистических данных.
Значение отрицательного критерия Стьюдента: практическое применение
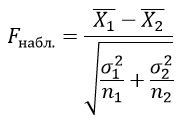
Практическое применение отрицательного критерия Стьюдента заключается в том, что он позволяет определить, есть ли значимые различия между двумя выборками. Например, его можно использовать для проверки эффективности нового лекарства путем сравнения двух групп пациентов: одна получает новое лекарство, а другая - плацебо.
Для применения отрицательного критерия Стьюдента необходимо собрать данные из двух выборок и посчитать среднее значение их разности. Затем на основе полученного значения можно сделать вывод об отрицательности эффекта в случае, если результаты второй выборки оказываются ниже первой.
Исходя из этого, отрицательный критерий Стьюдента можно использовать в таких ситуациях, как:
- Сравнение эффективности двух различных методов лечения;
- Оценка эффективности рекламной кампании;
- Изучение влияния фактора на выбор потребителей;
- Сравнение результатов эксперимента до и после применения изменений.
Таким образом, отрицательный критерий Стьюдента является важным инструментом в анализе данных и позволяет сделать выводы о наличии значимых различий между двумя выборками. Его практическое применение помогает в решении различных задач, связанных с проверкой гипотез и оценкой влияния различных факторов.
Применение отрицательного критерия Стьюдента в научных исследованиях
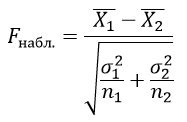
Применение отрицательного критерия Стьюдента в научных исследованиях имеет несколько этапов:
- Собрать данные по двум группам или условиям, которые требуется сравнить. Это могут быть результаты измерений, опросные данные и т.д.
- Проверить данные на выполнение условий применимости отрицательного критерия Стьюдента. Эти условия включают нормальность распределения данных и равенство дисперсий между группами. Для этого можно использовать специальные статистические тесты, например, тест Шапиро-Уилка для проверки нормальности распределения.
- Вычислить значение статистики отрицательного критерия Стьюдента. Это делается путем вычисления разности средних значений двух выборок, деленной на стандартную ошибку разности.
- Определить критическую область и сравнить значение статистики с этой областью. Если значение статистики попадает в критическую область, то можно отвергнуть нулевую гипотезу о равенстве средних. Если значение статистики не попадает в критическую область, то гипотезу о равенстве средних не удалось отвергнуть.
- Интерпретировать результаты. Если нулевая гипотеза отвергнута, это означает, что между группами или условиями существуют статистически значимые различия. Если нулевая гипотеза не отвергнута, это означает, что различия между группами или условиями не являются статистически значимыми.
Применение отрицательного критерия Стьюдента позволяет провести объективное и статистически подтвержденное сравнение двух выборок или условий в научных исследованиях. Этот метод является одним из самых распространенных и надежных способов выявления различий между группами и условиями, что позволяет делать выводы и обобщения на основе данных и статистических показателей.




