Пересечение отрезков — это одна из основных задач геометрии, которая заключается в определении того, пересекаются ли два отрезка на плоскости или нет. Понимание пересечения отрезков имеет большое значение в различных областях, таких как компьютерная графика, геодезия, архитектура и многих других.
Чтобы определить, пересекаются ли два отрезка, необходимо учитывать различные условия. Во-первых, концы отрезков должны лежать по разные стороны от прямой, образованной другим отрезком. Во-вторых, два отрезка могут пересекаться только в том случае, если они не параллельны и не лежат на одной линии. Дополнительным условием является нахождение общей точки пересечения между концами отрезков.
Например, пусть на плоскости имеются два отрезка АВ и СD. Если концы отрезков A и B находятся по разные стороны от прямой СD, а точка пересечения О не совпадает с концами отрезков, то можно сделать вывод, что отрезки АВ и СD пересекаются.
Зная условия и правила для определения пересечения отрезков, можно эффективно решать разнообразные задачи, связанные с геометрией. Это может быть как нахождение точки пересечения двух отрезков, так и построение графических моделей с учетом условий пересечения.
Что такое пересечение отрезков?
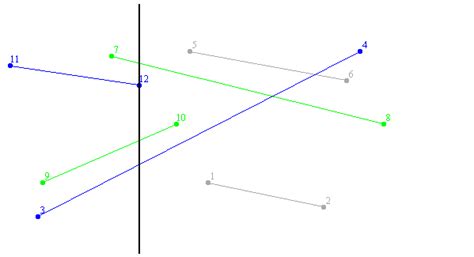
Для того чтобы отрезки пересекались друг с другом, необходимо выполнение следующих условий:
- Отрезки должны лежать на одной прямой. Это значит, что они не должны быть параллельными и не пересекать другие прямые.
- Отрезки должны иметь хотя бы одну общую точку, которая не является конечной точкой ни одного из отрезков.
Пересечение отрезков может иметь различные виды:
- Отрезки пересекаются внутри - общая точка отрезков находится между их конечными точками.
- Отрезки пересекаются вне - общая точка отрезков находится за пределами их конечных точек.
- Отрезки пересекаются частично - отрезки имеют общую точку только в одной из своих конечных точек.
- Отрезки не пересекаются - отрезки не имеют общих точек.
Пересечение отрезков является важным понятием в геометрии и находит применение в различных областях, таких как компьютерная графика, робототехника, алгоритмы и др.
Определение пересечения отрезков
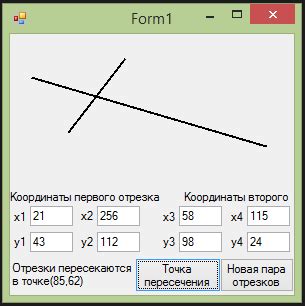
Для определения пересечения отрезков необходимо проверить выполнение следующих условий:
- Отрезки не могут быть параллельными - если два отрезка являются параллельными, то они не пересекаются. Для проверки параллельности можно использовать сравнение углов наклона отрезков.
- Проекции отрезков на оси координат пересекаются - если проекции отрезков на ось абсцисс пересекаются и проекции на ось ординат также пересекаются, то отрезки пересекаются.
Если оба условия выполняются, то отрезки пересекаются и содержат общую часть. В противном случае отрезки не пересекаются.
Пересечение отрезков имеет важное значение в различных областях, таких как компьютерная графика, алгоритмы и геометрические вычисления. Знание и понимание концепций пересечения отрезков позволяет эффективно решать различные задачи и проектировать алгоритмы, связанные с обработкой геометрических данных.
Условия, необходимые для пересечения отрезков

Чтобы два отрезка пересекались между собой, должны выполняться определенные условия:
- Отрезки должны лежать на одной прямой. Если отрезки лежат на разных прямых, то их пересечение невозможно.
- Отрезки должны иметь общую точку или пересекаться друг с другом. Если концы одного отрезка не попадают на другой отрезок и не пересекаются с ним, то отрезки не пересекаются.
- Длины отрезков не должны быть равны нулю. Если длина отрезка равна нулю, то это означает, что отрезок состоит только из одной точки и не может пересечься с другим отрезком.
- Если один отрезок полностью находится внутри другого, то они также считаются пересекающимися.
Условия для пересечения отрезков могут быть использованы для проверки на пересечение в программном коде или графических приложениях. Если все условия выполняются, то можно сделать вывод, что отрезки пересекаются, и выполнить необходимые действия.
Примеры пересечения отрезков
Давайте рассмотрим некоторые примеры пересечения отрезков.
Пример 1:
Пусть у нас есть два отрезка: AB с координатами A(1,3) и B(7,10), а также CD с координатами C(4,5) и D(8,7).
Отрезок AB представлен синим цветом, а отрезок CD - красным цветом.
На графике видно, что отрезки AB и CD пересекаются в точке E(6,6).
Пример 2:
Рассмотрим теперь отрезки EF и GH с координатами E(2,6), F(5,8) и G(4,4), H(7,7).
Отрезок EF представлен синим цветом, а отрезок GH - красным цветом.
На графике видно, что отрезки EF и GH не пересекаются.
Пример 3:
Пусть у нас есть отрезки IJ и KL с координатами I(1,4), J(4,7) и K(2,6), L(5,9).
Отрезок IJ представлен синим цветом, а отрезок KL - красным цветом.
На графике видно, что отрезки IJ и KL пересекаются в точке M(3,6).
Как вычислить пересечение отрезков?
- Первый отрезок должен иметь конечные точки A и B, а второй отрезок должен иметь конечные точки C и D.
- Точки A и B должны быть различными, аналогично точкам C и D.
- Отрезки не должны быть параллельными. На плоскости они должны иметь разные углы наклона.
- Если отрезки имеют общую точку, она должна находиться внутри обоих отрезков.
Для вычисления пересечения отрезков можно использовать различные алгоритмы, включая геометрические и аналитические методы. Один из таких методов - это вычисление уравнений прямых, на которых лежат отрезки, и сравнение значений их координат в общей точке.
Примером вычисления пересечения отрезков может служить следующая ситуация: у нас есть два отрезка AB и CD на плоскости, где точки A(1, 2), B(6, 4), C(3, 1) и D(8, 3). По условиям, отрезки не параллельны и имеют общую точку внутри себя. Мы можем вычислить пересечение отрезков и найти координаты общей точки.
Примечание: При использовании кода для вычисления пересечения отрезков рекомендуется проверять его на ошибки и особые случаи, такие как отрезки, лежащие на одной прямой или имеющие общие конечные точки.







