Пересекающиеся окружности - это две окружности, которые имеют некоторые точки пересечения. Эти точки могут быть различными и повлиять на свойства окружностей. В геометрии пересекающиеся окружности являются важным объектом и изучаются в контексте аналитической геометрии и теории колец.
Один из основных свойств пересекающихся окружностей - это то, что оси симметрии каждой окружности пересекаются в точке пересечения. Это означает, что если провести прямые линии через центры окружностей, эти линии будут пересекаться. Другое свойство состоит в том, что каждая окружность может быть рассматриваема как окружность, проходящая через центр другой окружности. Также стоит отметить, что пересекающиеся окружности имеют две точки пересечения, кроме случаев, когда они являются касательными.
Пример пересекающихся окружностей - это изображение на плоскости двух окружностей с различными радиусами и центрами, так что они пересекаются в двух точках. Это типичная ситуация, которая встречается в геометрии и может быть использована для решения различных задач и построения графиков.
В заключение можно сказать, что пересекающиеся окружности представляют собой важный объект изучения в геометрии. С их помощью можно решать различные математические задачи, выстраивать графики и анализировать структуру и свойства окружностей.
Что такое пересекающиеся окружности?

Когда пересекаются две окружности, обычно возникают две общие точки пересечения. Если окружности пересекаются в одной точке, то они называются касательными к друг другу.
Если окружности полностью совпадают, то они также будут пересекаться, и количество точек пересечения будет бесконечно много.
Пересекающиеся окружности являются важным элементом в геометрии и имеют множество свойств и применений. Они используются для решения различных задач, включая построение графиков, нахождение точек пересечения различных геометрических фигур, определение расположения объектов в пространстве и т.д.
| Свойства пересекающихся окружностей |
|---|
| 1. Окружности пересекаются в двух общих точках. |
| 2. Если окружности пересекаются в одной точке, они касаются друг друга. |
| 3. Окружности могут полностью совпадать. |
| 4. Центры пересекающихся окружностей лежат на одной прямой, проходящей через общие точки пересечения. |
| 5. При пересечении окружностей образуются равнобедренные треугольники. |
Определение и особенности
Основные особенности пересекающихся окружностей:
- Они могут иметь две, одну или ни одной точки пересечения в зависимости от расположения центров окружностей и их радиусов.
- Если две окружности имеют одну точку пересечения, то они называются касательными.
- Если две окружности не имеют точек пересечения, то они называются некасательными или не пересекающимися.
- Если окружности имеют две точки пересечения, то они называются пересекающимися и могут образовывать различные фигуры в зависимости от их радиусов и центров.
Пересекающиеся окружности встречаются как в геометрических задачах, так и в реальной жизни. Например, они используются в архитектуре для создания круглых многоугольников и встречаются в дизайне ландшафта.
Свойства пересекающихся окружностей
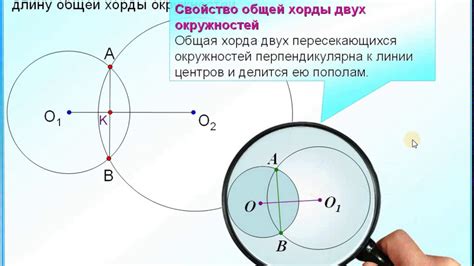
Пересекающиеся окружности представляют собой два или более круга, которые имеют общие точки пересечения. У таких окружностей есть несколько свойств, о которых следует знать:
| Свойство | Описание |
|---|---|
| Точки пересечения | Пересекающиеся окружности имеют две общие точки пересечения. В этих точках окружности "пересекаются" |
| Радиусы | Радиусы пересекающихся окружностей могут быть одинаковыми или разными. Если радиусы одинаковые, то окружности называются концентрическими окружностями |
| Центры | Центры пересекающихся окружностей могут находиться на одной прямой или быть смещены друг относительно друга |
| Дуги | Пересекающиеся окружности образуют две дуги между точками пересечения. Внешние дуги располагаются вне пересекающихся окружностей, а внутренние - находятся внутри этих окружностей |
| Тангенты | Касательные, проведенные к пересекающимся окружностям, пересекаются внешне или внутри окружностей, в которых их проводят |
Знание данных свойств позволяет более полно описать и анализировать пересекающиеся окружности. Эти свойства используются в геометрии, конструировании и других областях математики.
Геометрическая интерпретация
Пересекающиеся окружности в геометрии представляют собой две окружности, которые имеют хотя бы одну общую точку. Эта точка, называемая точкой пересечения, может быть единственной или их может быть больше одной.
Геометрическая интерпретация пересекающихся окружностей позволяет рассматривать их взаимное расположение. В зависимости от взаимного положения окружностей, можно выделить следующие случаи:
- Окружности пересекаются в двух точках. Этот случай называется пересечением.
- Окружности совпадают и имеют бесконечное множество общих точек.
- Окружности не пересекаются и не совпадают. В этом случае говорят о внешнем или внутреннем разлучении окружностей.
Геометрическая интерпретация пересекающихся окружностей широко применяется в геометрических задачах и построениях. Например, она может быть использована для определения таких элементов, как точки пересечения прямых, построения треугольников и четырехугольников, а также для решения различных задач о движении точек и фигур.
Примеры пересекающихся окружностей
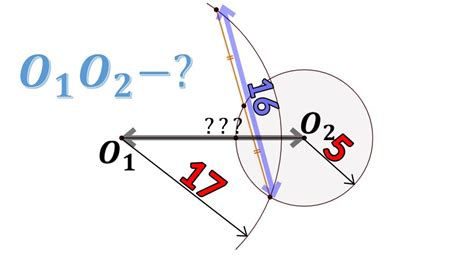
Пример 1: Окружности O1 и O2 с центрами в точках A и B соответственно. Они пересекаются в точках C и D. Расстояние между центрами окружностей равно расстоянию между точками C и D.
Пример 2: Окружности O1 и O2 с центрами в точках A и B соответственно. Они пересекаются в точке C. Расстояние между центрами окружностей меньше, чем расстояние от точки C до каждого из центров.
Пример 3: Окружности O1 и O2 с центрами в точках A и B соответственно. Они пересекаются в двух точках C и D. Расстояние между центрами окружностей больше, чем расстояние от точки C до каждого из центров.
Это лишь некоторые примеры пересекающихся окружностей, которые иллюстрируют различные возможные ситуации в их распределении в пространстве. Все эти примеры имеют множество приложений в различных областях знаний, таких как математика, физика, геометрия и др.
Уравнения пересекающихся окружностей

Для определения уравнений пересекающихся окружностей необходимо знать координаты и радиусы каждой из них. Пусть имеются две окружности: окружность O1 с центром в точке (x1, y1) и радиусом r1, и окружность O2 с центром в точке (x2, y2) и радиусом r2.
Уравнение окружности O1: (x - x1)2 + (y - y1)2 = r12
Уравнение окружности O2: (x - x2)2 + (y - y2)2 = r22
Пересечение двух окружностей происходит в тех точках, которые удовлетворяют обоим уравнениям. Для нахождения точек пересечения можно решить систему уравнений, состоящую из этих двух уравнений. Решение системы позволит определить координаты точек пересечения, если они существуют.
Зная уравнения двух пересекающихся окружностей, можно провести их графическое представление на координатной плоскости и найти точки пересечения путем их построения. Таким образом, можно наглядно представить геометрический смысл пересекающихся окружностей.
Пример уравнений пересекающихся окружностей:
O1: (x - 3)2 + (y - 2)2 = 4
O2: (x - 6)2 + (y - 4)2 = 9
В данном примере окружности O1 и O2 пересекаются в двух точках. Их координаты можно найти, решив систему уравнений:
(x - 3)2 + (y - 2)2 = 4
(x - 6)2 + (y - 4)2 = 9
Решением данной системы будет две точки пересечения (x1, y1) и (x2, y2), которые можно подставить в уравнения окружностей, чтобы убедиться в их корректности.
Расчет точек пересечения
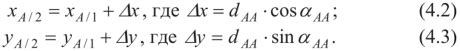
Для расчета точек пересечения двух окружностей необходимо найти координаты этих точек в пространстве. Существуют несколько методов для выполнения этой задачи.
Одним из методов является использование системы уравнений, в которых неизвестными являются координаты точек пересечения. Уравнения формируются на основе свойств пересекающихся окружностей.
Представим две окружности с центрами (x1, y1) и (x2, y2) и радиусами r1 и r2 соответственно. Тогда уравнения, описывающие эти окружности, имеют вид:
| (x - x1)^2 + (y - y1)^2 = r1^2 |
| (x - x2)^2 + (y - y2)^2 = r2^2 |
Решение этой системы уравнений позволит найти координаты точек пересечения окружностей.
Если уравнения имеют два различных корня, то это означает, что окружности пересекаются в двух точках. Если уравнения имеют один корень, то это означает, что окружности соприкасаются в одной точке. Если уравнения не имеют корней, то окружности не пересекаются.
При расчете точек пересечения окружностей необходимо учитывать возможность возникновения ошибок округления, так как значения координат точек могут быть дробными числами.
Теорема о существовании двух точек пересечения
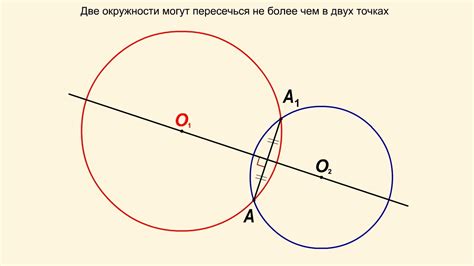
Теорема о существовании двух точек пересечения гласит, что для любых двух пересекающихся окружностей существуют всегда две точки пересечения.
Данная теорема базируется на свойствах окружностей и геометрии. Пересекающиеся окружности обычно имеют центры, расположенные на разных расстояниях друг от друга. Каждая из окружностей также имеет определенный радиус. Простое геометрическое рассуждение позволяет утверждать, что две окружности с различными радиусами и разными центрами должны пересекаться в двух точках.
Для доказательства этой теоремы можно использовать таблицу, где каждая строка представляет свойство окружностей и их элементы:
| Свойство | Описание |
|---|---|
| Центр окружности | Точка, откуда исходят все возможные радиусы |
| Радиус окружности | Расстояние от центра окружности до любой ее точки |
| Пересечение окружностей | Общие точки, которые принадлежат обеим окружностям |
Из таблицы видно, что если у двух окружностей разные центры и радиусы, то у них обязательно должно существовать две точки пересечения. Это свойство является одним из основных при решении задач, связанных с пересекающимися окружностями.
Теорема о существовании двух точек пересечения имеет широкое применение в различных областях, включая геометрию, физику, инженерию и другие науки. Правильное понимание и применение этой теоремы позволяет решать сложные задачи и выявлять взаимосвязи между двумя пересекающимися окружностями.
Практическое применение

В геодезии пересечение окружностей используется для определения точного местоположения объектов на земной поверхности. С помощью специальных приборов и методов, геодезисты могут рассчитать координаты точек пересечения окружностей. Это позволяет определить точное положение пунктов геодезической сети или месторасположение геодезических измерений.
Еще одним примером практического применения пересекающихся окружностей является механика и строительство. В инженерных расчетах и проектировании конструкций, пересечение окружностей позволяет установить точки пересечения линий сил или плоскостей. Эти данные используются для анализа напряжения и определения максимальной нагрузки, которую может выдержать конструкция.
Также пересечение окружностей находит применение в компьютерной графике и алгоритмах. Он используется для определения областей пересечения объектов, заданных в виде окружностей, а также для решения задач визуализации и построения моделей.
В общем, практическое применение пересекающихся окружностей охватывает множество областей, от геодезии и механики до компьютерной графики и алгоритмов. Изучение свойств и способов вычисления пересечений окружностей является важной задачей для ученых и практиков во множестве сфер деятельности.




