Задача 5 класса Петерсона – это типичная задача, которую ученикам предлагают решать на уроках математики. Она обычно описывает реальную ситуацию или проблему, которую необходимо решить с помощью математической модели.
Построение математической модели в задаче 5 класса Петерсона начинается со сбора и анализа информации. Нужно понять, какие данные предоставлены в условии задачи и какие из них являются ключевыми для решения.
Далее необходимо выбрать подходящую математическую модель для решения задачи. Это может быть, например, уравнение, система уравнений, алгоритм или график. Важно выбрать модель, которая наиболее точно отражает ситуацию в задаче.
После выбора модели необходимо провести вычисления, используя заданные данные. Возможно, потребуется применить различные математические операции, такие как сложение, вычитание, умножение, деление или нахождение среднего значения. Необходимо также учесть единицы измерения и округление результатов.
В заключение, важно проанализировать полученные результаты и представить их в понятной форме. Это может быть ответ на вопрос в задаче или построение графика. Также стоит проверить правильность решения, проследив, что все используемые операции были выполнены правильно.
Построение математической модели
При решении задачи 5 класса Петерсона необходимо построить математическую модель, которая позволит нам формализовать условие и найти ответ.
Для начала, рассмотрим условие задачи и выделим в нем ключевые элементы. Затем определим переменные, которые будут использоваться в нашей модели.
Допустим, задача состоит в том, чтобы найти площадь прямоугольного участка, зная его длину и ширину. Длина участка обозначим как l, а ширину как w. Наша цель - найти значение переменной S, которая будет обозначать площадь участка.
Построим таблицу с переменными и их обозначениями:
| Переменная | Обозначение |
|---|---|
| Длина участка | l |
| Ширина участка | w |
| Площадь участка | S |
Теперь, зная обозначения переменных, мы можем записать математическую модель задачи:
S = l * w
Это уравнение позволяет нам выразить площадь участка через его длину и ширину.
Таким образом, мы построили математическую модель задачи, которая позволяет нам вычислить площадь прямоугольного участка, зная его длину и ширину.
Модель задачи 5 класс Петерсона
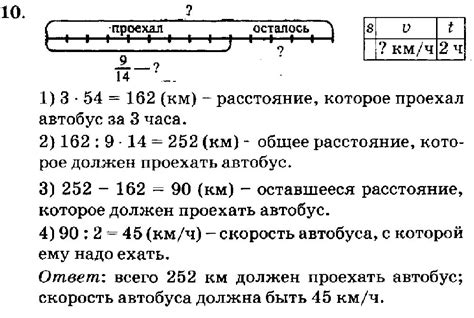
В данной задаче заданы условия и требуется найти решение. Часто такие задачи могут быть сформулированы в виде текста или схемы, которую нужно анализировать в поисках закономерностей и решения.
Математическая модель задачи 5 класс Петерсона обычно основана на использовании различных операций, таких как сложение, вычитание, умножение и деление, а также на работе с простыми уравнениями и неравенствами.
Решение задачи обычно состоит из нескольких шагов, каждый из которых поддерживается доказательством или аргументацией. Важно следить за логикой решения и правильно интерпретировать результаты.
В заключение, задача 5 класс Петерсона – это пример математической модели, которая помогает развить у учеников навыки анализа, логического мышления и работы с математическими операциями. Решение задачи требует использования различных математических инструментов и грамотного подхода к построению модели и интерпретации результатов.
Шаги построения модели

- Определите задачу, которую необходимо решить. В данном случае это задача из учебника Петерсона для 5 класса.
- Определите исходные данные, которые даны в условии задачи.
- Разберите условие задачи на составляющие и выполните их анализ. Возможно, потребуется применение различных математических концепций и формул.
- Составьте уравнение или систему уравнений, отражающих условие задачи.
- Проведите необходимые вычисления на основе построенной модели. Используйте математические методы и алгоритмы для решения уравнений и систем уравнений.
- Проверьте полученное решение и удостоверьтесь в его правильности. Для этого можно использовать обратную связь с исходными данными и условием задачи.
- Оформите результаты решения задачи в виде ответа и объяснения, чтобы их можно было легко понять и проверить.
При построении математической модели задачи важно строго следовать указанным шагам. Это поможет вам систематизировать информацию, правильно поставить уравнения и получить точное решение задачи.
Анализ условия задачи

Перед тем, как построить математическую модель задачи, необходимо тщательно проанализировать условие задачи. В задаче необходимо построить математическую модель в виде уравнения или неравенства, которое позволит решить поставленную задачу.
Условие задачи может содержать информацию о количестве предметов, их характеристиках, взаимодействиях, ограничениях и требованиях. Для более понятного анализа условия задачи, его можно разбить на отдельные составляющие и выделить ключевые факты и данные.
Важно обратить внимание на текст задачи и выделить основную информацию о предметах, их свойствах и взаимодействиях. Строить математическую модель нужно на основе этих данных.
Перед построением математической модели необходимо ответить на следующие вопросы:
- Какие объекты или предметы встречаются в задаче?
- Какие свойства или характеристики имеют эти объекты?
- Как они взаимодействуют друг с другом?
- Есть ли какие-либо ограничения или требования в задаче?
Анализ условия задачи позволяет понять, какие данные необходимо использовать при построении математической модели. Он предоставляет основу для определения величин и переменных, которые будут использоваться в уравнении или неравенстве.
Итак, важно тщательно проанализировать задачу, выделить ключевые факты и данные, понять взаимодействия объектов и определить ограничения. Это поможет построить правильную математическую модель, которая позволит решить поставленную задачу.
Идентификация переменных и функций

Перед тем как приступить к построению математической модели задачи, необходимо определить переменные и функции, которые будут использованы.
Переменные - это символы или буквы, которые обозначают неизвестные величины в задаче. Они позволяют нам работать с неизвестными числами или данными.
Функции - это математические выражения или правила, которые преобразуют переменные или другие значения в новые значения.
Для идентификации переменных и функций в задаче 5 класса Петерсона, мы можем использовать следующие обозначения:
- Зададим переменные A и B, которые будут обозначать неизвестные числа или величины в задаче.
- Функция С(A, B) будет представлять собой выражение или правило для расчета искомого значения в задаче.
После идентификации переменных и функций, мы сможем построить математическую модель задачи, используя эти символы и выражения.




