Уравнения — это математические выражения, в которых две величины или выражения считаются равными друг другу. Решение уравнений является важной частью математики, поскольку оно позволяет находить значения неизвестных переменных и решать различные проблемы.
Одним из методов решения уравнений является метод компонентных действий. Этот метод основывается на идее разбиения уравнения на части, выполняя одинаковые арифметические операции с обеими сторонами уравнения. Обычно в методе компонентных действий используются четыре основных действия: сложение, вычитание, умножение и деление.
Давайте рассмотрим пример уравнения и его решение с помощью метода компонентных действий. Рассмотрим уравнение: 2x + 5 = 13. Для решения этого уравнения нам необходимо избавиться от числа 5, чтобы найти значение переменной x. Чтобы это сделать, мы можем применить действие вычитания, вычитая 5 из обеих сторон уравнения. Таким образом, мы получим: 2x = 13 - 5, что дает нам 2x = 8.
Основные понятия уравнений

В уравнении могут присутствовать следующие элементы:
- Неизвестное число: это число, которое нужно найти. Обычно обозначается буквой, например, x, y или z.
- Известные числа: это числа, которые уже известны и заданы в условии уравнения.
- Операции: это математические действия, которые применяются к известным и неизвестным числам для получения конечного результата.
В процессе решения уравнений необходимо проводить определенные действия с числами, чтобы найти значение неизвестного числа. Основные операции, применяемые при решении уравнений, включают:
- Сложение и вычитание: сложение и вычитание применяются для изменения значений чисел в уравнении.
- Умножение и деление: умножение и деление используются для изменения значений чисел с целью упростить уравнение.
- Изменение знака: изменение знака позволяет изменить знаки чисел и перенести их на другую сторону уравнения.
При решении уравнений необходимо соблюдать определенные правила и последовательность действий. Важно помнить, что при выполнении операций на одну сторону уравнения необходимо выполнить такие же операции на другую сторону, чтобы сохранить равенство.
Изучение основных понятий уравнений позволяет легче понять и применять методы решения уравнений, проводить необходимые операции и получить точное значение неизвестного числа.
Классификация уравнений
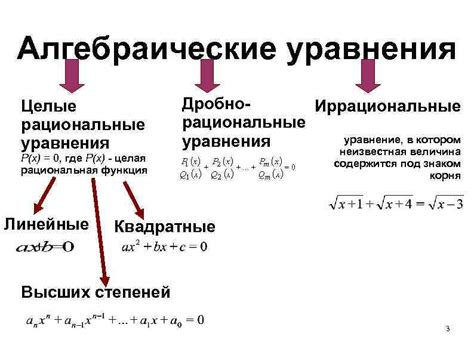
Уравнения могут быть классифицированы по различным критериям. Давайте рассмотрим основные классы уравнений:
1. Алгебраические уравнения - это уравнения, которые содержат алгебраические выражения, такие как многочлены. Примеры алгебраических уравнений: x^2 + 3x - 4 = 0, 2(x + 1) = 5.
2. Тригонометрические уравнения - это уравнения, которые содержат тригонометрические функции, такие как синус, косинус, тангенс и т. д. Примеры тригонометрических уравнений: sin(x) = 0.5, cos(x) + 2sin(x) = 0.
3. Логарифмические уравнения - это уравнения, которые содержат логарифмы. Примеры логарифмических уравнений: log(x) = 2, ln(x) + ln(x + 1) = 3.
4. Экспоненциальные уравнения - это уравнения, которые содержат экспоненты. Примеры экспоненциальных уравнений: 3^x = 27, 2^x - 2 = 10.
5. Разностных уравнений - это уравнения, которые задают зависимость между последовательными значениями функции. Примеры разностных уравнений: y_{n+1} - 2y_n = 5, y_{n+2} - y_n = 0.
6. Дифференциальные уравнения - это уравнения, которые задают зависимость между функцией и её производными. Примеры дифференциальных уравнений: y' + 2y = 0, d^2y/dx^2 + y = 0.
Это лишь некоторые из классов уравнений. В каждом из них применяются различные методы решения, и поэтому важно понять, к какому классу принадлежит данное уравнение, чтобы определить наиболее подходящий метод решения.
Разложение уравнений на компоненты

Для начала необходимо проанализировать уравнение и определить, какие действия нужно выполнить с его компонентами. Компоненты уравнения могут состоять из переменных, констант и различных операций (сложение, вычитание, умножение и деление).
Разложение уравнений на компоненты основывается на свойствах алгебры. Например, уравнение 2x + 3 = 7 может быть разложено на две компоненты: 2x и 3. Затем происходит поочередное решение каждой компоненты по правилам алгебры.
Процесс разложения уравнения на компоненты может быть сложным и требовать тщательного анализа. Однако, с практикой и знаниями алгебры, вы сможете легко определить компоненты уравнения и провести необходимые действия для их решения.
Важно понимать, что разложение уравнений на компоненты является только одной из стратегий решения уравнений. В некоторых случаях другие методы решения могут быть более эффективными. Поэтому, при решении уравнений рекомендуется ознакомиться с различными стратегиями и выбрать наиболее подходящий метод для каждого конкретного уравнения.
В заключение, разложение уравнений на компоненты является полезным инструментом при решении уравнений. Он позволяет упростить сложные уравнения и легко решить каждую компоненту по отдельности. Знание алгебры и практика помогут вам владеть этим методом и эффективно решать уравнения.




