Скрещивающиеся ребра – особенные элементы, которые можно наблюдать в структуре геометрических фигур, в частности, в кубе. Это рёбра, которые пересекают друг друга внутри фигуры. Изучение и понимание их смысла является важной частью геометрии и математической логики.
Знание о скрещивающихся ребрах позволяет углубиться в понимание особенностей пространства и геометрических фигур. Они являются ключевыми элементами для решения сложных задач и проведения глубокого анализа в различных областях, таких как архитектура, инженерия и компьютерная графика.
Одним из примеров использования скрещивающихся ребер является построение трехмерной графики. С помощью скрещивающихся ребер можно создавать сложные трехмерные модели, которые могут быть визуализированы на компьютере. Это позволяет разрабатывать и проектировать новые сооружения, технические устройства и другие объекты виртуально перед их физической реализацией.
Изучаем скрещивающиеся ребра кубов:
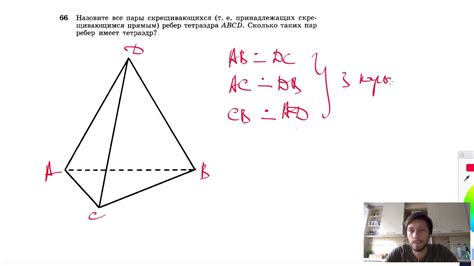
Скрещивающиеся ребра считаются одним из сложных и интересных аспектов кубо-челленджа. Они требуют от пользователя дополнительного внимания и навыков для решения. Скрещивающиеся ребра часто встречаются в различных методах сборки кубика Рубика.
Один из примеров скрещивающихся ребер - "создание креста". Этот этап решения кубика Рубика требует сборки креста на одной грани куба. Важно учесть, что при сборке креста необходимо соблюдать правильное расположение цветов ребер, чтобы образовались скрещивающиеся ребра.
Скрещивающиеся ребра требуют анализа и предвидения ходов, чтобы правильно решить эту часть головоломки. Они могут создать сложности даже для опытных куберсолверов, поэтому эта часть решения кубика Рубика требует практики и умения видеть глубину и связи между элементами головоломки.
Изучение и понимание скрещивающихся ребер кубов поможет вам улучшить свои навыки сборки, а также развить интуицию и логическое мышление. Захватывающий процесс решения головоломки кубика Рубика начинается с полного понимания всех ее элементов и этапов, включая скрещивающиеся ребра.
Понятие скрещивающихся ребер:
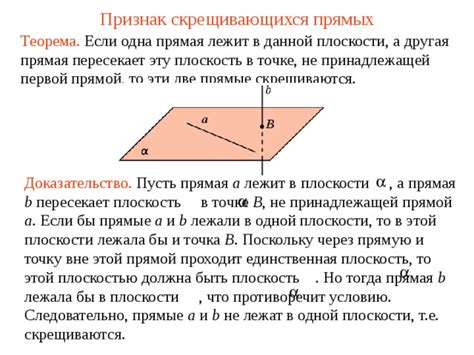
Паутинка скрещивающихся ребер в кубе образуется при сращивании четырех ребер на каждом из его углов. Каждая из этих площадок состоит из двух пересекающихся ребер, которые формируют пересечение в виде буквы "Х".
Скрещивающиеся ребра в кубе являются важным элементом в решении головоломки "Рубикова кубика". Они служат ориентирами и позволяют определить положение других элементов куба.
Понимание и умение работать со скрещивающимися ребрами помогает разбираться в логике кубика и находить оптимальные пути для его сборки.
Как образуются скрещивающиеся ребра:
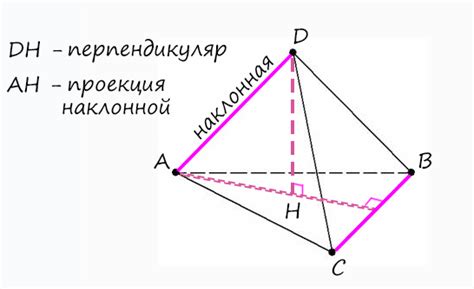
Скрещивающиеся ребра куба формируются путем соединения вершин, которые расположены на разных гранях. Такие ребра проходят через центральную точку куба, образуя диагональные линии.
Например, чтобы найти одно из скрещивающихся ребер, можно провести линию от вершины, расположенной на одной грани куба, к вершине на противоположной грани. Таким образом, получается скрещивающееся ребро, которое пересекает куб.
Скрещивающиеся ребра являются одной из особых характеристик куба и обладают уникальными свойствами. Они создают дополнительные связи и направления между различными элементами структуры куба.
Зависимость скрещивающихся ребер от позиции куба:

Позиция куба может сильно влиять на вид и расположение скрещивающихся ребер. Рассмотрим несколько примеров:
1. Если куб расположен таким образом, что одна из граней смотрит вверх, а другая грань находится справа, то скрещивающиеся ребра будут находиться на верхней и правой гранях. Это можно наглядно представить, если взять куб в руки и повернуть его соответствующим образом.
2. В случае, когда куб находится в положении, когда одна из граней смотрит вверх, а другая грань находится справа и слегка повернута, скрещивающиеся ребра будут находиться на верхней и правой гранях, но будут немного искривлены.
3. Если куб расположен таким образом, что одна из граней смотрит вверх, а другая грань находится и повернута влево, то скрещивающиеся ребра будут находиться на верхней и левой гранях. При этом, как и в предыдущих случаях, ребра могут быть искривлены.
Таким образом, позиция куба имеет значительное влияние на вид и расположение скрещивающихся ребер, и может быть использована для создания разнообразных комбинаций и узоров.
Практическое значение скрещивающихся ребер:
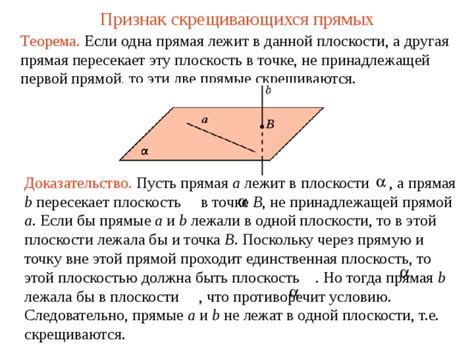
Скрещивание ребер образует сильную связь между сторонами куба, что способствует его устойчивости и прочности. Это дает возможность использовать куб для создания различных конструкций, как например, стеллажей, шкафов, столов, стульев и других предметов мебели.
Также скрещивающиеся ребра помогают в ориентации в пространстве. При сборке куба, скрещивающиеся ребра помогают определить правильное положение сторон и углов, что особенно полезно при создании сложных конструкций или при решении геометрических задач.
Понимание значения скрещивающихся ребер куба важно для обучения геометрии и математики в школе. Это позволяет ученикам лучше понять пространственные отношения и развивать навыки аналитического мышления.
Таким образом, скрещивающиеся ребра куба имеют практическое значение в различных областях, от строительства и мебельного производства до геометрии и математики. Они помогают создавать прочные конструкции и развивать пространственное мышление.
Примеры скрещивающихся ребер в реальной жизни:

1. Кристаллы:
В кристаллической структуре различных минералов и кристаллов часто можно наблюдать скрещивающиеся ребра. Например, в кристаллах кварца или флюорита эти ребра образуют прямые углы и дают кристаллу особый вид.
2. Архитектура:
В архитектуре можно встретить примеры скрещивающихся ребер в структуре зданий или мостов. Например, у исторических мостов или зданий в стиле готики встречаются ребра скрещивающихся арок, которые украшают и придают структуре прочность.
3. Рисунки и искусство:
В различных рисунках или произведениях искусства можно встретить скрещивающиеся ребра. Например, в геометрической абстракции или графических композициях используются ребра, которые пересекаются, чтобы создать интересную визуальную динамику.
Примеры скрещивающихся ребер в реальной жизни могут быть разнообразными и встречаются в различных областях, включая науку, искусство и архитектуру. Эти ребра придают объекту особый вид и структуру, а иногда и символическое значение.




