Трапеция - это геометрическая фигура, которая имеет две параллельные стороны, называемые основаниями, и две непараллельные стороны, называемые боковыми сторонами. В зависимости от своих свойств, трапеции делятся на различные типы. Одним из интересных свойств трапеции является условие, которое гласит, что диагонали этой фигуры взаимно перпендикулярны.
Что означает, что диагонали трапеции взаимно перпендикулярны? Перпендикулярность - это свойство линий, которые образуют прямой угол, то есть угол в 90 градусов. Если диагонали трапеции взаимно перпендикулярны, то они образуют прямые углы там, где пересекаются. Это означает, что верхняя и нижняя диагонали трапеции встречаются друг с другом под прямым углом.
Интересно отметить, что это свойство диагоналей трапеции может быть использовано для решения различных задач. Например, если известны длины оснований и угол между ними, можно найти диагонали трапеции. Также, зная длины диагоналей и угол между ними, можно найти длины оснований. Это является одним из примеров применения геометрии в реальной жизни.
В заключение, диагонали трапеции, которые взаимно перпендикулярны, образуют прямые углы между собой. Это свойство позволяет использовать геометрию для решения задач, связанных с этой фигурой. Понимание этого условия может помочь вам лучше понять геометрию трапеции и использовать ее в повседневной жизни.
Что такое трапеция и зачем нужны диагонали?
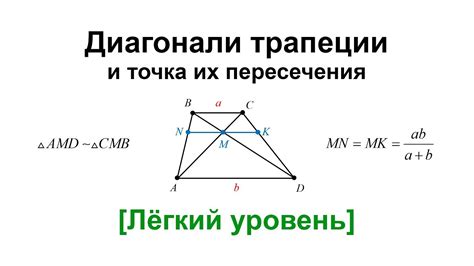
Если в трапеции диагонали взаимно перпендикулярны, это означает, что угол между диагоналями равен 90 градусов. Другими словами, диагонали пересекаются под прямым углом.
Зачем нужны диагонали в трапеции? Диагонали позволяют проводить дополнительные геометрические построения и находить различные свойства трапеции.
Например, если диагонали трапеции взаимно перпендикулярны, то они делят эту фигуру на четыре прямоугольных треугольника. Это свойство позволяет найти площадь трапеции, используя формулу для площади треугольника.
Также, если диагонали взаимно перпендикулярны, то их точка пересечения является центром вписанной окружности, которая описывает круг, построенный на длине сторон трапеции.
Таким образом, диагонали в трапеции играют важную роль в изучении и использовании различных свойств и формул этой геометрической фигуры.
Особенности трапеции
Особенностью трапеции является то, что ее диагонали взаимно перпендикулярны, то есть образуют прямой угол. Другими словами, если провести диагонали трапеции, то они будут пересекаться под прямым углом.
Для проверки перпендикулярности диагоналей трапеции можно воспользоваться теоремой Пифагора. Если квадрат длины одной из диагоналей равен сумме квадратов длин оснований, то диагонали перпендикулярны.
Также стоит отметить, что диагонали трапеции делят ее на четыре треугольника: два прямоугольных треугольника, образованных одной из диагоналей и основаниями, и два равнобедренных треугольника, образованных диагоналями и боковыми сторонами.
| Основания трапеции | Боковые стороны трапеции | Диагонали трапеции |
|---|---|---|
| Параллельны | Не параллельны и могут быть разной длины | Пересекаются под прямым углом |
Изучение особенностей и свойств трапеции помогает лучше понять ее геометрическую структуру и использовать в решении задач по геометрии.
Значение перпендикулярности диагоналей
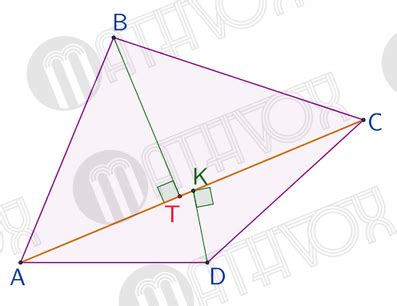
В трапеции диагонали считаются взаимно перпендикулярными, если они пересекаются под прямым углом. Это означает, что между диагоналями существует прямой угол, равный 90 градусам. Такая особенность влияет на свойства и характеристики трапеции.
Перпендикулярные диагонали в трапеции разделяют ее на четыре треугольника: два прямоугольных и два непрямоугольных. Четыре треугольника, образованные перпендикулярными диагоналями, имеют особые свойства.
- Прямоугольные треугольники, образованные перпендикулярными диагоналями, являются подобными. Это означает, что их соответствующие углы равны между собой, а соответствующие стороны пропорциональны.
- Сумма квадратов длин катетов прямоугольного треугольника, образованного перпендикулярными диагоналями, равна квадрату гипотенузы.
Таким образом, перпендикулярность диагоналей влияет на углы и стороны треугольников, образованных ими, позволяя нам сделать выводы о их свойствах. Это помогает в решении задач, связанных с определением различных параметров трапеции.
Следствия перпендикулярности диагоналей
Перпендикулярность диагоналей в трапеции имеет несколько важных следствий:
- Сумма квадратов длин боковых сторон трапеции равна сумме квадратов диагоналей. Данное свойство может быть использовано для решения задач на нахождение длины диагоналей или сторон трапеции.
- Диагонали делятся взаимно перпендикулярно.
- Если в трапеции диагонали взаимно перпендикулярны, то трапеция является равнобочной.
- Взаимная перпендикулярность диагоналей обусловливает равенство соответствующих углов треугольников, образованных этими диагоналями и боковыми сторонами трапеции.
Эти свойства дают возможность определить различные параметры трапеции и использовать их при решении геометрических задач. Также они являются основой для изучения других видов четырехугольников и построения различных фигур.
Примеры применения перпендикулярности диагоналей

Одним из основных примеров применения перпендикулярности диагоналей является нахождение площади трапеции. Если известны значения длин диагоналей и углов между ними, то можно использовать геометрическую формулу для расчета площади трапеции. Знание перпендикулярности диагоналей позволяет упростить этот расчет и использовать соответствующую формулу.
Также перпендикулярность диагоналей может помочь в нахождении значений других параметров трапеции, таких как углы, высоты или длины боковых сторон. Использование этого свойства позволяет сократить количество известных данных и упростить задачу.
Перпендикулярность диагоналей может быть полезна и в практических ситуациях. Например, при строительстве применение этого свойства позволяет корректно расположить стены или другие конструкции в трапециевидных помещениях. Это также может быть использовано при размещении мебели или при расчете площади пространств.
Таким образом, знание и использование перпендикулярности диагоналей трапеции имеет важные практические и теоретические применения в математике и повседневной жизни.
Математические свойства трапеции
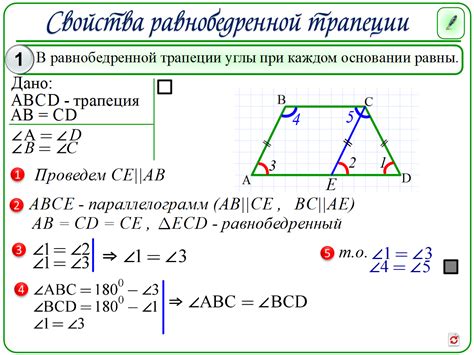
- Диагонали взаимно перпендикулярны. Это означает, что линии, соединяющие противоположные вершины трапеции, образуют прямые углы.
- Сумма углов трапеции равна 360 градусов. Так как противоположные углы трапеции совершенно не равны, то трапеция не является правильным многоугольником.
- Диагонали трапеции делят друг друга пополам. Это означает, что точка их пересечения, называемая точкой пересечения диагоналей, делит каждую диагональ на две равные части.
- Сумма длин двух углов в основании трапеции равна 180 градусов. Это означает, что если мы знаем два угла в основании, то третий угол автоматически становится определенным.
- Высота трапеции - это перпендикуляр, опущенный из вершины трапеции на параллельные стороны трапеции, либо на продолжение этих сторон. Формулой для расчета площади трапеции является произведение длины основания и высоты, деленное на 2.
Знание этих математических свойств трапеции позволяет лучше понимать ее геометрические особенности и использовать их при решении задач, связанных с трапециями.
Геометрические критерии перпендикулярности диагоналей
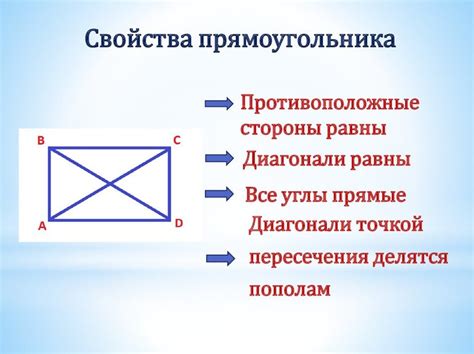
Геометрические критерии перпендикулярности диагоналей следующие:
1. Угол между диагоналями равен 90 градусам.
2. Взаимное перпендикулярное пересечение диагоналей образует четыре прямоугольных треугольника. В этом случае каждый из треугольников имеет хотя бы одну прямую угловую вершину.
3. Длины диагоналей связаны между собой по правилу Пифагора: квадрат длины одной диагонали равен сумме квадратов длин другой диагонали и половины разности квадратов боковых сторон трапеции.
Если диагонали трапеции взаимно перпендикулярны, то это свойство может быть использовано для доказательства ряда теорем, например, для вычисления площади трапеции или нахождения координат точек пересечения диагоналей.




