Высоты треугольника – это линии, соединяющие вершины треугольника с противоположными сторонами. Один из интересных аспектов, связанных с высотами треугольника, – это угол между ними. Этот угол является важной характеристикой треугольника и может дать много информации о его свойствах и симметрии.
Значение угла между высотами в треугольнике зависит от его типа. Например, в прямоугольном треугольнике угол между высотами всегда равен 90 градусов, так как противоположные стороны перпендикулярны. В остроугольном треугольнике этот угол меньше 90 градусов, а в тупоугольном – больше 90 градусов. Таким образом, угол между высотами является одним из признаков классификации треугольников по типу.
Особенностью угла между высотами в треугольнике является его связь с другими углами треугольника. Например, сумма углов между высотами и углами треугольника всегда равна 180 градусов. Это очевидно, так как высоты являются перпендикулярами к сторонам треугольника, и сумма углов в треугольнике равна 180 градусов.
Знание значения угла между высотами при анализе треугольников может помочь в решении задач на построение или доказательство определенных свойств треугольников. Также это понятие является важным для расчета площади треугольника с помощью формулы Герона или других способов. Поэтому изучение угла между высотами является неотъемлемой частью геометрии и строительства треугольников.
Определение угла между высотами
Для определения угла между высотами нужно провести высоты из вершин треугольника до противоположных сторон и затем измерить угол, образованный этими высотами. Обычно этот угол измеряется в градусах.
Угол между высотами может быть острый, прямой или тупой, в зависимости от его величины. Если угол между высотами острый, то он будет меньше 90 градусов. Прямой угол между высотами равен 90 градусам. Тупой угол между высотами больше 90 градусов.
Знание угла между высотами позволяет не только лучше понять форму и свойства треугольника, но и использовать его в решении задач разных областей, таких как геометрия, физика и строительство.
А вот небольшая интересная факт: в прямоугольном треугольнике угол между высотами всегда будет равен 45 градусам.
Значение угла между высотами в геометрии

Значение угла между высотами зависит от типа треугольника. В прямоугольном треугольнике он всегда равен 90 градусов, так как высота, проведенная к гипотенузе, является ее перпендикуляром. В остроугольном треугольнике угол между высотами может быть любым от 0 до 90 градусов. В тупоугольном треугольнике угол между высотами превышает 90 градусов и может быть больше либо меньше 180 градусов в зависимости от расположения вершин треугольника.
Знание значения угла между высотами позволяет решать различные задачи, связанные с нахождением площади треугольника, длиной сторон и других характеристик. Также угол между высотами может использоваться при построении геометрических моделей и конструкций.
| Тип треугольника | Значение угла между высотами |
|---|---|
| Прямоугольный | 90 градусов |
| Остроугольный | От 0 до 90 градусов |
| Тупоугольный | Больше 90 градусов |
Формула для вычисления угла между высотами
Угол между высотами в треугольнике можно вычислить с использованием формулы, известной как формула скалярного произведения или косинусового закона. Эта формула позволяет найти угол между двумя высотами, если известны длины этих высот.
Формула для вычисления угла между высотами выглядит следующим образом:
cos(угол) = (h1 * h2) / (l1 * l2)
где:
- угол - искомый угол между высотами
- h1 - длина первой высоты
- h2 - длина второй высоты
- l1 - длина стороны, которой соответствует первая высота
- l2 - длина стороны, которой соответствует вторая высота
Данная формула использует скалярное произведение векторов, чтобы найти значение угла между высотами. Она является основой для решения задач, связанных с определением углов треугольника по данным о высотах.
Применение формулы для вычисления угла между высотами позволяет более точно определить геометрические характеристики треугольника и использовать их в дальнейших расчетах и решении задач.
Свойства угла между высотами треугольника
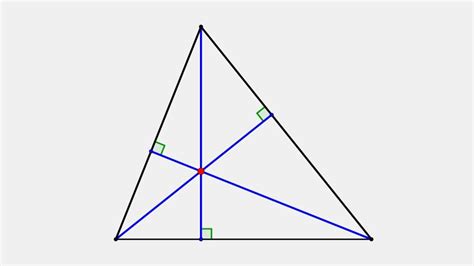
Основная особенность угла между высотами треугольника заключается в том, что его величина зависит от самого треугольника. То есть угол между высотами может быть разным для разных треугольников. Но существуют некоторые общие свойства, которые присущи всем треугольникам:
- Угол между высотами треугольника всегда острый или прямой. Это связано с тем, что высоты являются опорными отрезками, которые перпендикулярны сторонам треугольника и образуют прямые углы с ними.
- Угол между высотами треугольника может быть равным, меньшим или большим 90 градусов. Если все стороны треугольника равны, то угол между высотами будет равен 90 градусов. В остальных случаях он будет меньше 90 градусов.
- Угол между высотами треугольника никогда не может быть равным 180 градусов. Это связано с тем, что высоты не могут быть параллельными и в своем пересечении образовать угол, равный прямому. В таком случае было бы возможно построить треугольник с нулевыми сторонами, а это противоречит определению треугольника.
Знание свойств угла между высотами треугольника помогает в решении множества геометрических задач: вычисление площади треугольника, определение его типа (остроугольный, прямоугольный, тупоугольный), нахождение дополнительных углов и сторон треугольника.
Важно уделить достаточное внимание изучению данной темы, чтобы иметь полное представление о свойствах угла между высотами треугольника и применять их в практических задачах.
Угол между высотами в различных типах треугольников
В трактовке угла между высотами рассматривается угол, образованный двумя высотами треугольника, соединяющими общую вершину. Значение угла может быть разным в зависимости от типа треугольника.
В равностороннем треугольнике все стороны и высоты равны между собой, поэтому угол между высотами равен 60 градусов.
В равнобедренном треугольнике две стороны и две высоты равны между собой, поэтому угол между высотами также равен 60 градусов.
В прямоугольном треугольнике одна из высот является гипотенузой, а другая является катетом. Так как гипотенуза и катет перпендикулярны, то угол между высотами будет 90 градусов.
В остроугольном треугольнике угол между высотами может быть любым, от 0 до 90 градусов, в зависимости от соотношения сторон и углов треугольника.
В случае разностороннего треугольника значение угла между высотами может быть различным и зависит от конкретных значений сторон и углов треугольника.
Геометрическое значение угла между высотами
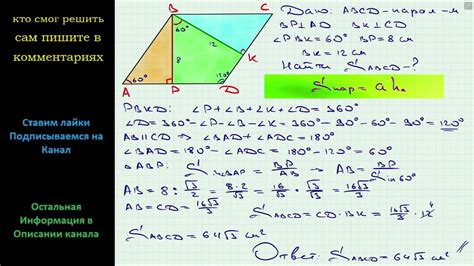
Главное свойство угла между высотами состоит в том, что он равен углу между сторонами треугольника, на которые эти высоты опущены. То есть, если мы обозначим угол между высотами как α, а углы, образованные высотами с соответствующими сторонами, как β и γ, то справедливо равенство α = β = γ.
Зная значение угла между высотами, можно решать различные задачи, связанные с треугольником. Например, он может быть использован для вычисления площади треугольника, если известны длины сторон и значения высот. Для этого можно воспользоваться формулой S = 0.5 * a * b * sin(α), где a и b - стороны треугольника, α - угол между высотами.
Угол между высотами также позволяет определить, является ли треугольник равнобедренным. Если угол между высотами равен 90°, это означает, что треугольник является прямоугольным. Если угол между высотами равен 60°, то треугольник равносторонний.
Обратим внимание, что угол между высотами может быть рассчитан только в случае, если треугольник не является прямоугольным или равносторонним. В этих случаях угол между высотами будет иметь значения 0° или 180° соответственно.
Примеры применения угла между высотами в практике

1. Конструкция зданий и мостов:
При проектировании и строительстве зданий и мостов инженеры используют угол между высотами для определения идеального положения столбов и опор. Знание этого угла позволяет распределить нагрузку равномерно и обеспечить устойчивость конструкции.
2. Геодезия и картография:
Угол между высотами также используется в геодезии и картографии для измерения и представления высотных различий на местности. Это помогает создавать точные карты рельефа и учитывать изменения высоты при разработке проектов.
3. Навигация и авиация:
При пилотировании самолетов угол между высотами является важной характеристикой при определении безопасной дистанции между летящими воздушными судами. Знание этого угла позволяет пилотам принимать правильные решения для избежания столкновений в воздухе.
Это лишь некоторые примеры применения угла между высотами, которые иллюстрируют его важность и практическую значимость. Понимание этого понятия позволяет решать различные задачи в области инженерии, геодезии, навигации и других областях, где требуется работа с пространственными объектами.
Приложения угла между высотами в различных областях

1. Геодезия:
В геодезии угол между высотами используется для расчета вертикальных компонент геодезических сетей, определения высот точек относительно исходного уровня и контроля уровня поверхностей при строительстве.
2. Физика:
В физике угол между высотами может быть использован для измерения углового положения объектов в пространстве. Например, в оптике он позволяет определить угол падения светового луча на поверхность и расчет отраженного или преломленного луча.
3. Архитектура:
В архитектуре угол между высотами используется для создания перспективных планов зданий, расчета пропорций и угловых отношений элементов конструкции. Он также помогает определить оптимальную высоту потолков и ракурсов освещения.
4. Аэронавтика:
В аэронавтике угол между высотами используется для определения положения самолета относительно земной поверхности, а также для расчетов трасс полета, планирования наборов и спусков высоты и определения оптимальных горизонтальных и вертикальных углов наклона.
5. Геология:
В геологии угол между высотами может быть использован для измерения уклона горных пород, определения угла промоин или наклона плоскостей разломов, что позволяет понять геологический строение местности и рассчитать геотехнические параметры.
Таким образом, понимание и применение угла между высотами имеет важное значение в различных областях, способствуя анализу и решению задач, связанных с пространственными отношениями, расчетами и проектированием.




