Угол лежащий против основания треугольника - это угол, образованный двумя сторонами треугольника, одной из которых является его основание. Такой угол обычно обозначается как угол BAC, где A и С - вершины треугольника, а B - точка на основании треугольника.
Угол BAC обладает несколькими важными свойствами. Во-первых, сумма углов, лежащих против основания треугольника, всегда равна 180 градусам. Это свойство известно как теорема об углах треугольника.
Второе свойство заключается в том, что угол BAC равен углу, образованному медианой треугольника, проведенной из вершины A, и отрезком, соединяющим вершину А с серединой основания BC. Это также известно как теорема о медиане треугольника.
Примечание: Угол, лежащий против основания треугольника, играет важную роль при решении задач по геометрии. Он помогает определить другие углы и длины сторон треугольника и использовать их свойства для решения различных задач.
Определение угла лежащего против основания треугольника

Угол лежащий против основания обычно обозначается буквой, которая соответствует вершине, где он находится. Например, если треугольник имеет вершины A, B и C, а основание - сторону AB, то угол лежащий против основания обозначается как угол C.
Углы, лежащие против основания треугольника, обладают различными свойствами. Например, сумма углов, лежащих против основания, всегда равна 180 градусам. Это следует из свойства суммы углов треугольника, согласно которому сумма всех углов в треугольнике равна 180 градусам.
Кроме того, если треугольник равнобедренный, то углы, лежащие против одинаковых сторон, будут равны между собой. Например, в равнобедренном треугольнике углы, лежащие против основания, будут равны.
Знание определения и свойств угла, лежащего против основания треугольника, помогает в анализе треугольников и решении геометрических задач. Оно также используется при рассмотрении теорем и доказательств, связанных с треугольниками.
Что такое угол лежащий против основания?

Угол лежащий против основания является активным элементом в определении и свойствах треугольника. Он помогает определить другие углы и стороны треугольника, а также решать различные задачи, связанные с геометрией.
Основание треугольника – это любая его сторона, к которой проведена высота. Углы, лежащие против основания, могут быть как острыми, так и тупыми. Например, в прямоугольном треугольнике прямой угол всегда будет лежать против гипотенузы.
Важно отметить, что высота, проведенная к основанию треугольника, является кратчайшим расстоянием от вершины до основания. Свойства угла лежащего против основания зависят от типа треугольника: остроугольного, тупоугольного или прямоугольного.
Как определить угол лежащий против основания треугольника?
Угол, лежащий против основания треугольника, называется продольным углом. Он находится между основанием и противоположной стороной треугольника.
Продольный угол можно определить с помощью теоремы синусов. Эта теорема гласит, что отношение длины стороны к синусу противолежащего ей угла равно постоянному значению для всех сторон треугольника:
a / sin(A) = b / sin(B) = c / sin(C)
Где a, b и c - длины сторон треугольника, A, B и C - величины соответствующих углов.
Чтобы определить продольный угол, необходимо знать длины основания треугольника и противоположной стороны, а также величину одного из других углов треугольника. Подставим эти значения в теорему синусов и получим значение синуса продольного угла.
Затем можно использовать тригонометрическую функцию arcsin (обратный синус), чтобы найти размер продольного угла.
Например, если известны длина основания треугольника (a = 5), длина противоположной стороны (b = 7) и величина угла (C = 60 градусов), то можно выразить значение синуса продольного угла следующим образом:
sin(A) = (b * sin(C)) / a
Используя тригонометрическую функцию arcsin, можно найти значение угла:
A = arcsin((b * sin(C)) / a)
Таким образом, зная длину основания треугольника, длину противоположной стороны и величину одного из других углов, можно определить продольный угол с помощью теоремы синусов.
Свойства угла лежащего против основания треугольника

Угол, лежащий против основания треугольника, имеет несколько свойств:
- Угол лежащий против основания равнобедренного треугольника равен углу между равными сторонами треугольника.
- Угол лежащий против основания равнобедренного треугольника равен половине суммы двух углов основания треугольника.
- Сумма углов, лежащих против оснований треугольника, всегда равна 180 градусов.
- Угол лежащий против наибольшей стороны треугольника является наибольшим углом треугольника.
- Угол лежащий против наименьшей стороны треугольника является наименьшим углом треугольника.
Зная свойства угла лежащего против основания треугольника, можно проводить различные вычисления и находить неизвестные величины треугольников.
Угол лежащий против основания и его меры
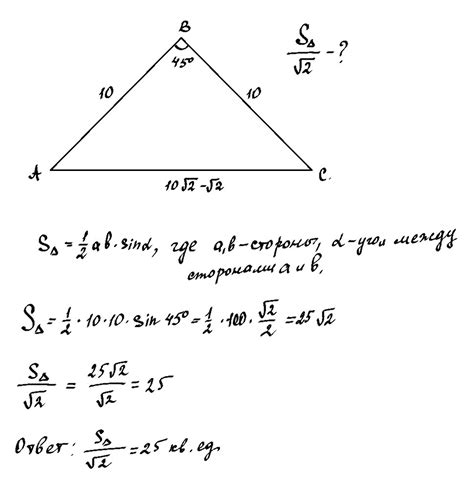
Мера угла лежащего против основания может быть определена с помощью различных методов. Одним из самых распространенных является использование тригонометрических функций. Мера угла может быть выражена в радианах или в градусах. Радианы используются в математике и физике, а градусы - в геометрии и тригонометрии.
Угол лежащий против основания треугольника имеет определенные свойства. В частности, если треугольник равнобедренный, то угол, лежащий против основания, также является равным. Также, если треугольник прямоугольный, то угол лежащий против гипотенузы будет прямым.
Знание углов, лежащих против основания треугольника, является важным для решения задач и вычислений связанных с этой фигурой. Оно позволяет определить соотношения между сторонами треугольника и вычислить его площадь, периметр и другие параметры.
Важно помнить, что углы, лежащие против основания треугольника, играют важную роль в его форме и свойствах. Чем больше эти углы, тем тупее треугольник. Если углы лежащие против основания равны, то треугольник будет равнобедренным. Если все углы треугольника равны, то он будет равносторонним.




