В 7-ом классе ученики начинают изучение алгебры, и одной из основных тем, которой они учатся, являются уравнения. Уравнение представляет собой математическое выражение, в котором присутствует неизвестная величина. Найти значение этой неизвестной - задача решения уравнения. В процессе изучения уравнений, ученики узнают, что некоторые уравнения не имеют корней.
Корни уравнения - это значения неизвестной величины, при подстановке которых уравнение становится верным. То есть, корни являются решениями уравнения. Когда уравнение не имеет корней, это означает, что нет значений неизвестной, при которых уравнение было бы верным.
Нет корней у уравнения, когда решение противоречит математическим правилам или логической природе уравнения. Например, если уравнение содержит дробь с нулевым знаменателем, оно будет не иметь корней. Также уравнение может быть противоречивым, если оно включает в себя какие-либо неправдивые утверждения.
Важно понимать, что отсутствие корней у уравнения не означает, что оно недостижимо или неинтересно. Уравнения без корней могут иметь важное значение в математике и науке, и их изучение помогает учащимся развивать логическое мышление и аналитические навыки.
Понимание того, что уравнение не имеет корней, является важной частью математического образования в 7-ом классе. Это помогает ученикам узнавать особенности уравнений и развивать навыки в поиске корректных решений. Знание этого понятия будет полезно не только в школьной программе, но и во многих других областях, где математика играет важную роль.
Что означает отсутствие корней у уравнения в 7-ом классе?

Корни уравнения – это значения неизвестной величины, при которых уравнение становится верным. Если уравнение имеет решение, то эти значения называются корнями уравнения.
В 7-ом классе мы изучаем различные типы уравнений и их решение. Но иногда бывает так, что уравнение не имеет решений, то есть не имеет корней.
Отсутствие корней может быть обусловлено несколькими причинами:
- Уравнение неверное. Если при решении уравнения получается противоречие, например, 3 = 5, то такое уравнение не имеет корней, потому что нет значений неизвестной величины, которые бы удовлетворяли этому условию.
- Уравнение не имеет действительных корней. Некоторые уравнения могут иметь только комплексные корни, которые невозможно представить в виде действительных чисел, например √-1. В 7-ом классе мы еще не рассматриваем комплексные числа, поэтому в рамках этого курса мы говорим о действительных корнях уравнений.
- Уравнение противоречиво. Иногда уравнение может иметь параметры, значения которых противоречат друг другу. Например, x^2 = -1, в данном случае нет действительных корней, так как нет значения x, при котором квадрат этого числа равен -1.
Важно помнить, что отсутствие корней не означает, что уравнение является неправильным или неверным. Просто в данном случае уравнение не имеет действительных решений.
В 7-ом классе мы изучаем основы алгебры и учимся решать различные типы уравнений, как с одной неизвестной, так и с несколькими. Понимание понятия корней уравнения является важной составляющей в процессе обучения алгебре.
Понятие уравнения и его корней

Корни уравнения – это значения переменных, при которых уравнение принимает истинное значение. Если уравнение имеет хотя бы один корень, то оно называется корневым уравнением.
Если уравнение не имеет корней, это означает, что для данного уравнения нет таких значений переменных, при которых оно станет верным. В общем случае это может означать, что график функции или линии уравнения не пересекает ось абсцисс.
Уравнения без корней могут возникать, например, при решении уравнений вида x^2 + 1 = 0, где нет реальных значений переменных, при которых выражение становится равным нулю.
Учебный план 7-го класса и обучение уравнениям
Уравнение без корней означает, что данное уравнение не имеет решений, то есть значение переменной, которое удовлетворяет уравнению, не существует. Это может иметь место в случае, когда уравнение противоречит математическим правилам или условиям задачи.
На уроках алгебры в 7-м классе учащиеся изучают основы решения уравнений, такие как линейное уравнение вида "ax + b = 0". Они учатся находить значение переменной, которое удовлетворяет уравнению и делает его верным.
В процессе обучения учащиеся узнают, что уравнение может иметь один корень, два корня или даже бесконечно много корней. Однако, в некоторых случаях, уравнение не имеет ни одного корня. Это означает, что не существует значения переменной, которое удовлетворяет уравнению.
Непонимание этого понятия может привести к ошибкам при решении уравнений и неправильному ответу. Поэтому, при изучении алгебры и решении уравнений, важно осознавать, что уравнение может быть либо решаемым, либо не иметь корней.
В 7-м классе учащиеся получают базовые знания и навыки в области решения уравнений, которые впоследствии будут углубляться в старших классах. Понимание понятия "уравнение без корней" является важным шагом в освоении алгебры и последующих математических тем.
Простейшие линейные уравнения в 7-ом классе

В 7-ом классе учатся решать такие уравнения. Они обычно имеют вид ax + b = 0, где a и b - это числа, а x - неизвестное значение переменной.
Чтобы найти решение уравнения, нужно избавиться от терма с неизвестной переменной и найти значение переменной, при котором уравнение станет верным.
Если решая уравнение, мы получаем какое-либо число, то это означает, что уравнение имеет один корень. Если мы получаем противоречие или нет решения, то уравнение не имеет корней.
Если же уравнение не имеет корней, это означает, что график линейной функции, заданной этим уравнением, не пересекает ось абсцисс. Решение такого уравнения невозможно найти в обычных вещественных или рациональных числах.
Понимание отсутствия корней у уравнения
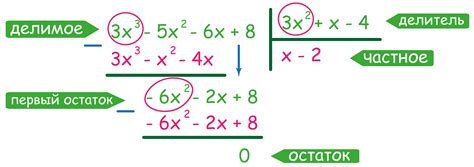
Уравнение, которое не имеет корней, означает, что не существует такого значения переменной, при котором уравнение станет истинным. Иными словами, решений у такого уравнения нет.
В седьмом классе обычно изучаются линейные, или первой степени, уравнения, которые можно записать в форме ax + b = 0, где a и b - заданные числа, а x - переменная.
Если уравнение имеет решение, то это значит, что существует такое значение переменной x, которое удовлетворяет уравнению. Если же решения нет, то уравнение не имеет корней.
Например, рассмотрим уравнение 2x + 3 = 7. Чтобы найти корень, нужно избавиться от постоянного члена справа от знака равенства, вычтя его из обеих частей уравнения. Получим: 2x = 4. Затем делим обе части уравнения на коэффициент при переменной x: x = 2. Итак, уравнение имеет один корень.
Теперь рассмотрим уравнение 2x + 3 = 8. Выполняем аналогичные операции: вычитаем 3 и получаем 2x = 5, затем делим на 2 и получаем x = 2,5. В этом случае уравнение имеет один корень.
Но вот уравнение 2x + 3 = 9 не имеет решений. Если мы вычтем 3 из обеих частей уравнения, получим 2x = 6, а при делении на 2 мы получим x = 3. Но если мы подставим значение x = 3 обратно в исходное уравнение, мы увидим, что оно неверное: 2*3 + 3 ≠ 9. Таким образом, уравнение не имеет корней.
Такое понимание отсутствия корней у уравнения важно для правильного решения математических задач и успешного продвижения в изучении математики.
Математическая терминология и понятие "корень" в уравнениях

В математике понятие "корень" используется для обозначения значений переменных, при подстановке которых в уравнение оно становится истинным. Если уравнение имеет корень, то это означает, что существует такое значение, которое при подстановке в уравнение даёт верное равенство. Если же уравнение не имеет корней, то это означает, что нет таких значений переменных, которые при подстановке сделают уравнение верным.
Простой пример уравнения с одним корнем: x + 5 = 9. В данном случае, значение переменной x равняется 4, так как при подстановке этого значения в уравнение получаем верное равенство 4 + 5 = 9.
Если уравнение имеет более одного корня, то это означает, что существует несколько значений, которые при подстановке в уравнение дают верное равенство. Например, уравнение x^2 = 16 имеет два корня: x = 4 и x = -4. При подстановке обоих значений равенство будет выполняться: 4^2 = 16 и (-4)^2 = 16.
Также возможна ситуация, когда уравнение не имеет корней. Это означает, что не существует таких значений переменных, которые при подстановке сделают уравнение верным. Например, уравнение x^2 + 1 = 0 не имеет корней, так как не существует такого значения переменной x, при котором равенство x^2 + 1 = 0 выполнялось бы.
Почему могут отсутствовать корни у уравнения в 7-ом классе?
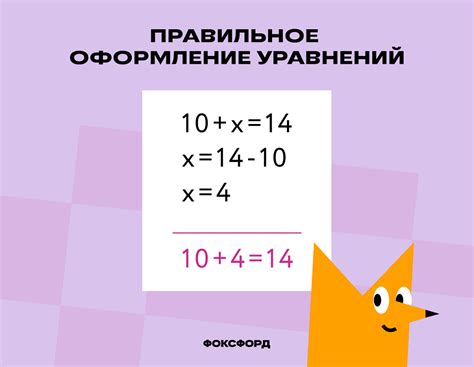
Уравнение без корней означает, что уравнение не имеет решений в виде действительных чисел. Такое может произойти по нескольким причинам:
- Уравнение может быть противоречивым, то есть его решениями являются противоположные значения, которые невозможно удовлетворить одновременно.
- Уравнение может иметь комплексные корни, то есть корни, которые являются мнимыми числами. В 7-ом классе мы еще не изучаем комплексные числа, поэтому в рамках данного уровня образования уравнение может считаться не имеющим корней.
- Уравнение может быть некорректно поставлено, например, равенство может быть записано неправильно или несовместимо с другими условиями задачи.
В каждом из этих случаев уравнение не имеет действительных корней в 7-ом классе. Однако, в более продвинутых курсах математики и при изучении комплексных чисел можно найти корни для некоторых из этих уравнений.
Решение уравнений в 7-ом классе без корней

Однако, некоторые уравнения могут не иметь корней. Это означает, что нет таких значений переменных, при которых оба выражения в уравнении становятся равными. Такие уравнения считаются неразрешимыми.
Уравнение может не иметь корней по различным причинам. Например, если в уравнении присутствуют квадратные или кубические корни, то они могут быть комплексными числами, что означает, что уравнение не имеет решений в вещественных числах.
Другой причиной может быть то, что оба выражения в уравнении противоречат друг другу и не могут быть равными ни при каких значениях переменных. Например, уравнение "2x + 5 = 2x + 7" не имеет решений, потому что нет таких значений переменной x, при которых 2x + 5 будет равно 2x + 7.
В контексте 7-ого класса, уравнения без корней могут использоваться для тренировки учеников в решении уравнений и развитии логического мышления. Ученикам предлагается анализировать уравнение и прийти к заключению, что оно не имеет решений. Это помогает развить умение работать с уравнениями и понимать различные возможные случаи в их решении.




