Уравнение с бесконечным множеством корней — это уравнение, которое имеет бесконечно много различных значений переменной, удовлетворяющих условию данного уравнения. Это означает, что любое значение переменной является корнем такого уравнения.
Простейшим примером уравнения с бесконечным множеством корней является тождество, где переменная исключена и условие справедливо для всех значений. Например, уравнение "2 + 2 = 4" является уравнением с бесконечным множеством корней, так как оно выполняется для любых значений переменной.
Однако, уравнение с бесконечным множеством корней может быть и более сложным. Например, уравнение "x^2 - 4 = 0" имеет бесконечно много корней, так как для всех натуральных чисел x, равных 2 или -2, это уравнение будет выполняться.
Уравнения с бесконечным множеством корней находят свое применение в математике, физике и других науках. Они могут использоваться для решения определенных задач и моделирования сложных явлений. Понимание этого понятия позволяет более глубоко изучать и применять математические и научные методы.
Определение уравнения с бесконечным множеством корней

Один из примеров уравнения с бесконечным множеством корней - уравнение вида x = k, где k - любое число. В этом случае любое число k удовлетворяет условию, что x равно k, и является корнем уравнения.
Также уравнение с бесконечным множеством корней может появиться, когда в нем присутствуют переменные с удвоенным значением, например, x^2 = 4x. Это уравнение имеет бесконечное множество корней, так как любое значение x, равное 0 или 4, удовлетворяет условию и является решением.
Важно отметить, что уравнения с бесконечным множеством корней могут возникать в различных областях математики и науки. Они могут быть полезны для моделирования и решения сложных задач, а также для создания математических моделей, описывающих неоднозначные ситуации.
Понимание концепции уравнений с бесконечным множеством корней позволяет математикам и ученым более точно анализировать и решать различные задачи, связанные с уравнениями и моделями. Это также способствует развитию абстрактного и логического мышления, что является важным аспектом в области математики и науки.
Уравнение с бесконечным количеством решений

Одним из примеров уравнения с бесконечным множеством корней является тождество. Тождество - это уравнение, которое выполняется для любых значений переменных. Например, уравнение "x = x" является тождеством. В этом уравнении любое число является решением, так как оно всегда равно самому себе.
Еще одним примером уравнения с бесконечным множеством корней является уравнение "sin(x) = 0". В этом случае, синус угла равен нулю для всех углов, кратных 0 и 180 градусов, то есть для всех значений x вида x = n * π, где n - целое число.
Такие уравнения встречаются в различных областях математики и физики. Они могут использоваться для решения определенных задач, а также для доказательства различных теорем и свойств.
| Примеры уравнений с бесконечным множеством решений |
|---|
| x = x |
| sin(x) = 0 |
| 2x + 4 = 2(x + 2) |
Уравнение с бесконечным множеством решений может быть полезным, когда требуется найти все возможные значения переменных или когда нужно доказать некоторое свойство уравнения или системы уравнений.
Уравнение, имеющее бесконечные корни
В математике существуют уравнения, которые могут иметь бесконечное количество корней. Такие уравнения называются уравнениями с бесконечным множеством корней.
Одним из примеров такого уравнения является тождественное уравнение. Тождественное уравнение – это уравнение, которое выполняется для любого значения переменной. В таком уравнении все значения переменной являются его корнями. Например, уравнение x = x является тождественным уравнением, так как оно выполняется для любого значения x.
Другим примером уравнения с бесконечным множеством корней является квадратное уравнение с нулевым дискриминантом. В квадратном уравнении, общий вид которого выглядит как ax^2 + bx + c = 0, дискриминант определяет количество и тип корней уравнения. Если дискриминант равен нулю, то уравнение имеет два одинаковых вещественных корня или один вещественный корень кратности два. Если дискриминант равен нулю и коэффициент c также равен нулю, то уравнение имеет бесконечное множество корней. Например, уравнение x^2 = 0 имеет бесконечное множество корней, так как для любого значе
Особый случай уравнения с бесконечными решениями
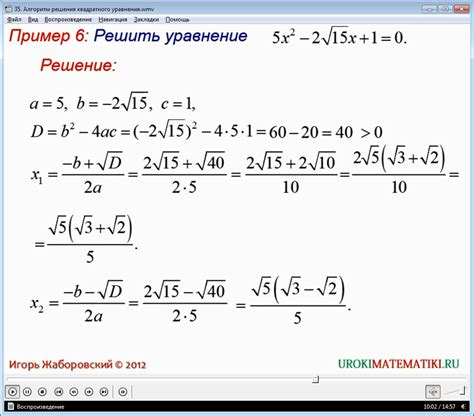
Например, рассмотрим уравнение x = x. В этом случае любое значение переменной x будет удовлетворять уравнению. Если мы возьмем x = 1, уравнение верно: 1 = 1. Если мы возьмем x = 2, уравнение также верно: 2 = 2. Мы можем продолжать бесконечно подставлять различные значения для x, и уравнение все равно будет истинным.
Этот особый случай уравнения с бесконечными решениями возникает, когда обе стороны уравнения равны друг другу, и результат всегда истинен. Такие уравнения иногда называются тождественными уравнениями или идентичностями.
Если встречается уравнение с бесконечным количеством решений, то это означает, что любое значение переменной будет являться решением уравнения.
Специфика уравнения с бесконечным множеством корней

Определение уравнения с бесконечным множеством корней:
Уравнение с бесконечным множеством корней - это уравнение, которое истинно для любого значения переменной. Такие уравнения не имеют определённых значений переменной, когда удовлетворяются определённые условия.
Примеры уравнений с бесконечным множеством корней:
- 1 + x = x
- x^2 = x
- cos(x) = cos(2x)
Что делать при решении уравнения с бесконечным множеством корней:
При решении уравнения с бесконечным множеством корней важно учитывать, что оно не будет иметь конкретных решений. Вместо этого необходимо найти условия, при которых исходное уравнение будет истинно. Это может быть достигнуто путем нахождения значений переменной, при которых обе стороны уравнения равны друг другу.
Анализ и использование уравнения с бесконечным множеством корней:
Уравнения с бесконечным множеством корней могут быть полезны для изучения симметрии и периодичности функций, а также для анализа математических моделей. Они обычно возникают в задачах, связанных с гармоническими функциями, циклическими процессами и периодическими колебаниями. Также он может быть введен в процессе решения других уравнений, когда появляются экстра-решения.
Примеры уравнений с бесконечно большим числом решений

Например, рассмотрим уравнение x^2 - 1 = 0. Это уравнение имеет два простых корня: x = -1 и x = 1. Однако, если мы умножим оба корня на любое число n, получим бесконечно много решений, так как (-1)^2 - 1 = 0 и (1)^2 - 1 = 0 для любого n.
Другим примером уравнения с бесконечным множеством корней является уравнение x^3 - 8 = 0. В этом уравнении есть один простой корень x = 2. Однако, если мы возведем это решение в любую четную степень, то оно также будет являться корнем данного уравнения. Например, (2^2)^3 - 8 = 0 и (2^4)^3 - 8 = 0 для любой четной степени.
Таким образом, уравнения с бесконечным множеством корней могут иметь бесконечное число решений, которые удовлетворяют условиям данного уравнения. Это связано с особенностями степенных функций и их способностью образовывать бесконечные последовательности чисел, удовлетворяющие уравнению.
Ситуации, в которых возникают уравнения с бесконечным количеством корней

Одна из ситуаций, где возникают уравнения с бесконечным количеством корней, - это уравнение прямой линии. В случае, когда уравнение имеет вид y = kx, где k - любое число, график этой функции будет прямой линией, проходящей через начало координат. В данном случае, каждая точка на линии является корнем уравнения, и их количество является бесконечным.
Также, уравнения с бесконечным количеством корней могут возникать в случаях функций, которые имеют периодическую природу. Например, уравнение синусоиды y = sin(x) имеет бесконечное количество корней, так как функция периодична и проходит через нулевую точку в каждой точке, кратной 2π.
Еще одной ситуацией, где возникают уравнения с бесконечным количеством корней, - это уравнения экспоненциальных функций. Например, уравнение y = 0, где 0 - это основание экспоненты, будет иметь бесконечное количество корней, так как любая точка на оси x становится корнем уравнения.
Такие ситуации, когда возникают уравнения с бесконечным количеством корней, представляют интерес в математике и имеют важное значение при изучении графиков функций и решении уравнений. Это позволяет лучше понять свойства функций и их взаимосвязь с уравнениями.
Математические примеры уравнений с бесконечным множеством решений

Одним из примеров уравнения с бесконечным множеством решений является уравнение вида x = c, где c - произвольная константа. Например, уравнение x = 2 имеет бесконечное количество решений, так как любое значение x = 2 удовлетворяет уравнению.
Еще одним примером уравнения с бесконечным множеством решений является уравнение вида 2x = 2x + 1. В данном случае, раскрывая скобки и сокращая члены, получаем тождество 0 = 1. Так как это тождество неверно, уравнение не имеет конкретного решения, но имеет бесконечное количество решений в виде произвольных значений x.
| Уравнение | Бесконечное множество решений |
|---|---|
| x = c | Да |
| 2x = 2x + 1 | Да |
Такие уравнения являются особенными и могут быть использованы в различных математических моделях и задачах. Они демонстрируют, что не все уравнения имеют конкретные значения решений, и иногда могут существовать бесконечное количество возможных значений, соответствующих условиям уравнения.
Когда возникают уравнения с бесконечным количеством решений

Такие уравнения могут возникать в различных случаях. Например, если уравнение содержит только переменные без коэффициентов и констант, то решениями будут все значения переменной из соответствующего диапазона. Другим примером могут быть уравнения, в которых присутствуют тригонометрические функции или логарифмы.
Также уравнения с бесконечным количеством решений могут возникать при наложении ограничений на переменные. Например, если в уравнении присутствует операция деления на ноль или логарифм от нуля.
Уравнения с бесконечным количеством решений требуют особого подхода при решении. Их решение может включать в себя нахождение общего вида решения и определение диапазона значений переменной, в котором все решения существуют.
Важно понимать, что уравнения с бесконечным множеством решений могут иметь различные интерпретации и быть связаны со специфическими ситуациями или свойствами рассматриваемой системы.




